О чем статья

Абсолютная величина и свойства модуля

Определение

Абсолютная величина или модуль $x$ (обозначается $|x|$ ) называется отрицательное число, что совпадает с $x$ , если $x\geq{0}$ и взятое со знаком минус, если $x < 0$ , то есть

$|x| = \left\{ = \begin{aligned} x\\ -x \end{aligned} \right$

(1)

В первом уравнении $x$ , если $x\geq{0}$ , а во втором уравнении $-x$ , если $x < 0$ .

Например, $|+5| = +5 = 5$ , $|-3| = -(-3) = 3$ , $|0| = 0$ .

Есть такие свойства модулей:

$|x| = |-x|$

(2)

$x\geq{0}$ , тогда согласно (1) $|x| = x$ . В это же время $-x < 0$ , поэтому из первого свойства получается $|-x| = -(-x) = x$ Значит $|x| = |-x|$ . Теперь пусть $x < 0$ , тогда из (1) имеем $|x| = -x$ . В то же время $-x > 0$ , поэтому $|-x| = -x$ . Значит $|x| = |-x|$ .

$x\leq{|x|$ , $-x\leq{|x|}$

(3)

Доказательство неравенства (3).

а) Если $x > 0$ , тогда в первом соотношении $x = |x|$ , а во втором – $-x < |x|$ .

б) Если же $x < 0$ , тогда $x < |x|$ , а $-x = |x|$ .

$|x + y|\leq{|x| + |y|$

(4)

Аналогично можно доказать (4).

Пусть:

а) $x + y > 0$ тогда согласно (1) $|x + y| = x + y$ , а согласно (3) дальше у нас получается $x + y \leq{|x| + |y|$ .

б) $x + y < 0$ , поэтому снова согласно (1), (3), и (2) имеем:

$|x + y| = -(x + y) = (-x) + (-y)\leq{|-x| + |-y| = |x| + |y|}$ .

Свойство доказано.

$||x| - |y||\leq{|x - y|}$

(5)

Доказательство неравенства (5).

$|x| = |x - y + y| = |(x - y) + y|\leq$ [согласно (4)] $\leq{|x - y| + |y|\to|x| - |y|\leq{|x - y|}$ .

Аналогично:

$|y| = |y - x + x| = |(y - x) + x|\leq|y - x| + |x| = |x - y| + |x|\to\\{\to}{|y| - |x|\leq{|x - y|}$ .

Так как $||x| - |y|| = ||y| - |x||$ , тогда из полученных соотношений получается неравенство (5).

$|xy| = |x| * |y|$

(6)

По определению модуль произведения чисел $x$ и $y$ равен либо $x$ x $y$ , если $x * y\geq{0}$ , либо -( $x$ x $y$ ), если $x$ x $y < 0$ . Из правил умножения действительных чисел следует, что произведение модулей чисел $x$ и $y$ равно либо $x$ x $y$ . $x * y \geq{0}$ , либо $-(x * y)$ , если $x * y < 0$ . что доказывает рассматриваемое свойство.

Рассмотрим (7) свойство:

Модуль частного от деления $x$ на $y$ = частному от деления модуля числа $x$ на модуль числа $y$

$\mid{x\over {y}}\mid = {|x|\over{|y|}}$ , где $y\neq{0}$

(7)

Так как частное ${x\over{y}}$ = ${x} * {1\over{y}}$ , тогда ${\mid{x\over {y}}} = {\mid{x} * {1\over{y}}$

Определение и свойство вышеперечисленных модулей применяются при исследовании функций, построения их графиков, решения уравнений и неравенств с модулями.

Геометрические свойства абсолютной величины

Если смотреть с точки зрения геометрической абсолютной величины, тогда модуль вещественного (действительного) или комплексного чисел находится расстояние между числом и началом координат. Рассмотрим комплексные и вещественные (действительные числа.

Вещественные числа

Область определения – это $-\infty, +\infty)$ .
Область значений – $[0, +\infty)$ .
Чётная функция.
Функция дифференцируема везде, кроме нуля. Если точка $x = 0$ , тогда функция претерпевает излом.

Комплексные числа

Область определения, то есть, вся комплексная плоскость.
Область значений – $[0, +\infty)$ .
Модуль как комплексная функция ни в одной точке не дифференцируема

Обратим внимание, что абсолютной величине можно дать геометрическое объяснение: если задать на числовой оси $OX$ точку с абсциссой $x$ , тогда $|x|$ – это расстояние этой точки $x$ к точке $O$ .

Алгебраические свойства абсолютной величины

Для любых вещественных чисел $x, y$ имеют место такие соотношения:

$|x| = \sqrt{x}^{2} = x * sgn {x} = max$ = { $x, -x$ }.
$a\leq{|a|$ .
$-|a| \leq{a}$ .
Квадрат модуля числа равен квадрату этого числа: $|a|^{2} = a^{2}$ .
Только тогда $a = 0$ , когда $|a| = 0$ , но модуль совершенно любого числа равен или же больше нуля: $|a| \geq{0}$ .
Модули противоположных чисел всегда равны: $|- a| = a$ .
Модуль произведения, где есть от двух чисел всегда равен произведению их модулей.
Модуль частного от деления двух чисел равен частному от деления модулей этих двух чисел: $\mid{x\over {y}}\mid = {|x|\over{|y|}}$ .
Постоянный положительный множитель можно выносить за знак модуля: $|ab| = a|b|, a> 0$ .
$|a + b|\leq{|a| + |b|}$ .
$|a - b|\leq{|a| - |b|}$ .
$|a| - |b|\leq{|a| + |b|}$ .
$|a\pm{b}|\geq{||a| - |b||$ .
$|a^{k}| = |a|^{k}$ , если $a^{k}$ существует.

Примеры решения задач с модулем

Пример 1

Задача

1) Построить график функции $y = |x|$ .

2) Решить уравнение $|x| = a, a > 0$ .

3) Решить неравенство $|x| = \leq{a}, a > 0$ .

4) Решить неравенство $|x| > a, a > 0$ .

Решение

Сначала построим график функции $y = |x|$ , а за основу берём (1) неравенство:

$y = |x| = \left\{ \begin{aligned} -x\\ x \end{aligned} \right$

(8)

При этом в первом уравнении $-x$ , если $x < 0$ , а $x$ , если $x\geq{0}$ . Поэтому графиком функции $y = |x|$ будет ломаная, см. рис. 1.

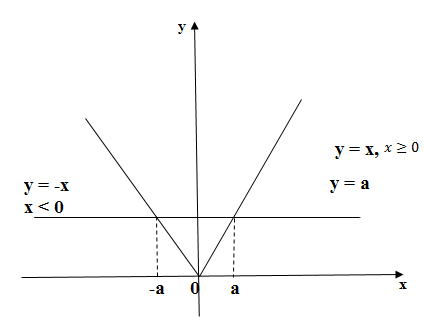
Абсолютная величина

Рис. 1

2) Первую часть задания выполнили, то есть, график построили а теперь нам необходимо решить уравнение $|x| = a, a > 0$ .

Пользуясь изображением выше (рис. 1) по формуле (8) решим сначала уравнение $|x|= a$ на интервале $-\infty < x < 0$ . Так как $|x| = -x$ , тогда $|x| = a\to{-x} = a\to{x} = -a$ .

Если же $0\leq{x}\leq{+\infty}$ , тогда $y = |x| = x$ , поэтому $|x| = a\to{x} = a$ .

Если $a = 0$ , тогда у нас получается единственное решения $x = 0$ .

Решили уравнение и получилось, что $x = -a$ , $x = a\quad{a > 0}$ .

Обратим ваше внимание, что решения $x = -a$ и $x = a$ легко понять по рис. 1. А если выходить из геометрического содержания абсолютной величины, тогда очевидно, что на расстоянии $|x| = a$ от точки $0$ на оси $OX$ находятся две точки $x = -a$ и $x = a$ .

3) Решаем неравенство $|x| = \leq{a}, a > 0$ .

Можно осуществить на каждом из интервалов $(-\infty, 0)$ и $0, +\infty$ или проще воспользоваться нашим уже построенным рисунком, из которого видно, что график ломаной $y = |x|$ находится не выше прямой $y = a, a > 0$ для $-a\leq{x}\leq{a}$ , то есть

$|x|\leq{a}\longleftrightarrow{-a}\leq{x}\leq{a}$ , где $a > 0$

(9)

4) Итак, решаем последнее неравенство $|x| > a, a > 0$ .

Запишем, согласно с рис. 1:

$|x| > a \longleftrightarrow{x}\in{(-\infty, -a)}\cup (a, +\infty), a > 0$ .

(10)

Соотношение (9) и (10) будут использоваться и в дальнейшем.

Ответ

Решили уравнение и у нас получилось: $x = -a$ , $x = a\quad{a > 0}$ ;

Из первого неравенства получилось, что $|x|\leq{a}\longleftrightarrow{-a}\leq{x}\leq{a}$ , где $a > 0$ .

Второе неравенство – $|x| > a \longleftrightarrow{x}\in{(-\infty, -a)}\cup (a, +\infty), a > 0$ .

Пример 2

Задача

Записать без знака модуля для функции $y = |x + 2|$ . Построить её график.

Решение

Приравняем подмодульное выражение к нулю $x + 2 = 0\to{x} = -2$ .

Теперь разделим ось на два интервала $I = (-\infty, -2)$ и $II = (-2, +\infty)$ .

Абсолютная величина

Если $x\in{I}$ , тогда $x + 2 < 0$ , поэтому, согласно с (1) $|x + 2| = -(x + 2)$ .

Если же $x\in{II}$ , тогда $x + 2 > 0$ , поэтому $|x + 2| = x + 2$ . Значит

$y = |x + 2| = \left\{ \begin{aligned} -x - 2, x\in{(-\infty, -2),\\ x + 2, x\in[2, +\infty). \end{aligned} \right$

Строим отдельно графики: $y = -x - 2$ для $x\in{(-\infty, -2)}$ и $y = x + 2$ для $x\in{[-2, +\infty)$ . (см. рис. 2)

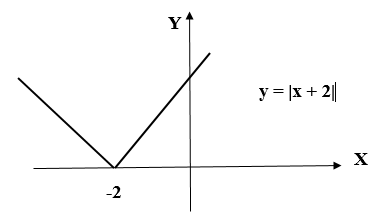
Абсолютная величина

Рис. 2

Мы видим, что график функции $y = |x + 2|$ можно получить параллельным переносом графика $y = |x|$ влево вдоль оси $OX$ на две единицы.

Очевидно, что по большому счёту график функции $y = |x - b|$ можно получить параллельным переносом графика $y = |x|$ по направлению оси $OX$ на $b$ единиц вправо, если $b > 0$ и влево, если $b < 0$ .

Как и в примере 1 после построения графика $y = |x - b|$ можно легко найти решение уравнения $|x - b| = a, (a > 0)$ , а также неравенств $|x - b| < a, |x - b| > a$ .

Ответ

Запишем: $y - |x - b|$ = $|x - b| = a, (a > 0)$ и неравенство $|x - b| < a, |x - b| > a$ .

Пример 3

Задача

Построить график функции $y = |x + 2| + |x - 3|$ .

Решение

Аналогично предыдущему примеру, приравняем к нулю подмодульное выражение: $x + 2 = 0\to{x = -2}; x - 3 = 0\to{x = 3}$ .

Разбиваем на три интервала:

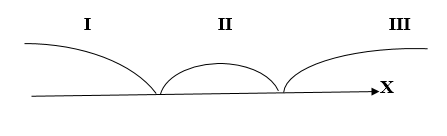
Абсолютная величина

1. Если $x\in{(-\infty, -2)}$ , тогда $x + 2 < 0, x - 3 < 0$ , поэтому $|x + 2| = -(x + 2), |x - 3| = -(x - 3})$ ,

$y = |x + 2| + |x - 3| = -x - 2 - x + 3 = -2x + 1$ .

2. Если $x\in{[-2, +3)$ , тогда $x + 2 \geq{0}$ и $|x + 2| = x + 2$ , а $x - 3 < 0$ и $|x - 3| = -x + 3$ , поэтому $y = |x + 2| + |x - 3| = x + 2 - x + 3 = 5$ .

3. Если $x\in{[+3, +\infty)$ , тогда $x + 2 > 0, x - 3 \geq{0}$ , поэтому $y = x + 2 + x - 3 = 2x - 1$ .

Значит, для нашей функции имеем:

$y = \left\{ \begin{aligned} -2x + 1{x}\in{(-\infty, -2),\\ 5 {x}\in[-2, 3)\\ 2x - 1{x}\in{[3, +\infty, \end{aligned} \right$

её график см. на рис. 3.

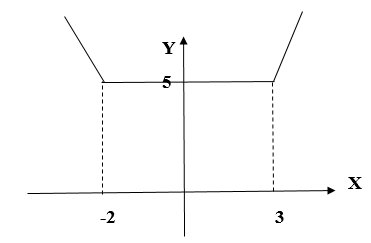
Абсолютная величина

Рис. 3

Нашли ошибку? Выделите текст и нажмите CRTL + Enter

Филипп Х.

Редактор.

Копирайтер, коммерческий автор, писатель, сценарист и автор-универсал в широком смысле.

Sergey Proshak:

30 декабря 2019 в 11:53

|x-y|≤|x|-|y|. Если х и у разных знаков неравенство не правильное.

Ответить

Добавить комментарий Отменить ответ

Игорь на Искусственный интеллект и робототехника: как они взаимодействуют и влияют друг на другаЕсть третий вариант: Пиар этой отрасли ради её дальнейшего финансирования преувеличивает возможности ИИ в конструктивной сфере. ИИ не обладает реальным
Игорь на Кибернетика и теория эволюции: взаимосвязь, принципы и моделированиеПредлагаю ознакомиться с несколько иным взглядом на отношения кибернетики и теории эволюции. Это статья "Синтез структуры организованных систем как центральная
АЛЕКСЕЙ РЫБАКОВ на Искусственный интеллект и робототехника: как они взаимодействуют и влияют друг на другаДавно в интернете задаю вопрос и не получаю ответа : Учёные бьются над созданием роботов копирующих людей . (проблемы ,
Торгын на Язык газеты: особенности и стиль в сравнении с другими СМИСпасибо, очень полезная статья, спасибо автору.
валентин на Свойства пространства и времени: открываем тайны физической реальностиСкорость света это скорость течения времени и в каждой точке пространства разная. Градиент сжатия пространства по вертикали определяет скорость течения