Декартова система координат, прямоугольная система в двух и трехмерном пространстве

О чем статья

Декартова система координат

Определение

Совокупность базиса $\overrightarrow{l_1}$ , $\overrightarrow{l_2}$ , $\overrightarrow{l_3}$ общей точки $O$ называют декартовой системой координат. Точка $O$ называется началом координат (см. на рис. 1).

Рисунок 1 - декартова система координат

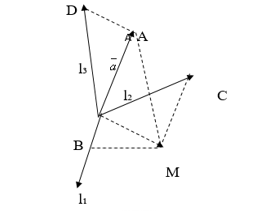
Рис. 1

Иногда такую систему называют косоугольной.

Нужна помощь в написании работы?

Мы - биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Прямоугольная декартова система координат

Прямоугольная система координат – это прямолинейная система, где взаимно перпендикулярны оси на плоскости или в пространстве. Такая система координат самая простая и поэтому часто используется

Среди декартовых систем, самая распространённая прямоугольная декартова система координат, которая бывает двух видов:

прямоугольная декартова система координат на плоскости;
прямоугольная система координат в пространстве.

Прямоугольная система координат на плоскости (двухмерная система координат)

Прямоугольная система координат на плоскости – это две взаимно перпендикулярные оси координат, которые пересекаются в точке $O$ (начало координат). Ещё такая система координат называется двухмерной. Есть ось $OX$ , которая направлена вправо и есть ось $OY$ , которая направлена вертикально вверх.

Координаты любых точек на плоскости $yOx$ определяются двумя числами $x, y$ . Эти числа – ортогональные проекции точки на соответствующие координатные оси. Как правило, $x$ – абсцисса точки, а $y$ – ордината (см. рис. 2). Элементарно можно найти расстояние между этими двумя точками:

$A(x_1y_1)$ и $B(x_2y_2)$ расстояние на плоскости определяется выражением:

$d = \overline{|AB|} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$

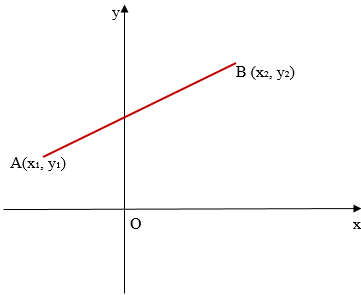
Графическое изображение - декартова система координат

Рис. 2

Прямоугольная система координат в пространстве (трёхмерная система координат)

Прямоугольная система в пространстве – это три взаимно перпендикулярные оси $OX, OY, OZ$ с общим началом в точке $O$ – началом координат. Ось $OX$ называется осью абсцисс, $OY$ – ось ординат, $OZ$ – ось аппликат.

Координата любой точки в пространстве определяется тремя настоящими числами $x, y, z$ . Часто такую систему называют: “прямоугольная система координат в трёхмерном пространстве”.

Расстояние между двумя точками находится по формуле:

$d = \overline{|AB|} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}$

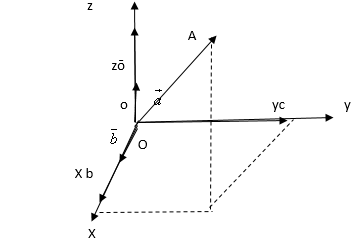
Рис. 2 - декартова система координат

Рис. 3

Вместо произвольных базисных векторов $\overrightarrow{l_1}$ , $\overrightarrow{l_2}$ , $\overrightarrow{l_3}$ удобнее взять единичные векторы $\overrightarrow{o}$ , $\overrightarrow{b}$ , $\overrightarrow{a}$ , направленные соответственно вдоль осей $OX, OY, OZ$ . Такие векторы называются ортами, а образованный ними базис называется ортонормированными (ортогональными). Вектор $\overrightarrow{a}$ = $\overrightarrow{OA}$ , который называется радиусом-вектором точки $A (x, y, z)$ и у него такой расклад:

$\overrightarrow{a} = x\overrightarrow{b} + y\overrightarrow{c} + z\overrightarrow{o} = (x, y, z).$

(3)

Очевидно, что произвольная точка $A(x, y, z)$ в заданной системе координат однозначно определяется своим радиусом-вектором $\overrightarrow{OA}$ , а координаты точки с координатами её радиуса-вектора.

Обратим внимание на тот факт, что, если в предыдущих темах выражение “дан вектор” мы подразумевали его графическое (геометрическое) изображение, то теперь выражение “дан вектор” необходимо воспринимать как задание тройке упорядоченных числе $(x, y, z)$ – координат вектора.

Решение задач

Пример

Задача

Убедиться, что система векторов $l_1, l_2, l_3$ образует базис и найти координаты вектора $\overline{a}$ в этом базисе, если известны в прямоугольной системе координаты этих векторов: $\overline{l}_{1} = (-1, 4, -1)$ , $\overline{l}_{2} = (4, -1, 1)$ , $\overline{l}_{3} = (8, 1, 0)$ , $\overline{a} = (9, -9, 5)$ .

Решение

Векторы $\overline{l}_{1}, \overline{l}_{2}, \overline{l}_{3}$ образуют базис, если они линейно независимы, то есть, их линейна комбинация $\lambda_{1}\overline{l}_{1} + \lambda_{2}\overline{l}_{2} + \lambda_{3}\overline{l}_{3} = 0$ , где $\overline{0} = (0, 0, 0)$ , только тогда, когда $\lambda_{1} = \lambda_{2} = \lambda_{3} = 0$

Проверим это при помощи свойств с темы базиса:

$\lambda_{1} * (-1, 4, -1) + \lambda_{2} * (4, -1, 1) + \lambda_{3} * (8, 1, 0) = (0, 0, 0) \to(-\lambda_{1}, 4\lambda_{1}, -\lambda) + (4\lambda_{2}, -\lambda_{2}, \lambda_{2}) + (8\lambda_{3}, \lambda_{3}, 0 * \lambda_{3}) = (0, 0, 0)\to(\lambda_{1} + 4\lambda_{2} + 8\lambda_{3}, 4\lambda_{1} - \lambda_{2} + \lambda_{3}, - \lambda_{1} + \lambda_{2}) = (0, 0, 0)$ .

Приравнивая соответствующие координаты, получим систему:

$\left\{ \begin{aligned} -\lambda_{1} + 4\lambda{2} + 8\lambda+{3} = 0\\ 4\lambda_{1} - \lambda_{2} + \lambda_{3} = 0\\ -\lambda_{1} + \lambda_{2} + 0 * \lambda_{3} = 0 \end{aligned} \right$

Определитель этой системы:

$\Delta = \begin{vmatrix} -1&4&8\\ 4&-1&1\\ -1&1&0 \end{vmatrix} = -4 + 32 - 8 + 1 = 21\neq{0}. \right$

Все вспомогательные определители $\Delta{\lambda}_{1} = \Delta{\lambda}_{2} = \Delta{\lambda}_{3} = 0$ , так как в каждом из них есть нулевой столбец из свободных членов однородной системы. Значит, согласно формулам Крамера $\lambda_{1} = \lambda_{2} = \lambda_{3} = 0$ , и, таким образом, векторы $\overline{l}_{1}, \overline{l}_{2}, \overline{l}_{3}$ – линейно независимы, а значит, создают новый базис.

Обратим внимание, что элементы столбцов определителя $\Delta$ совпадают с соответствующими координатами векторов $\overline{l}_{1}, \overline{l}_{2}, \overline{l}_{3}$ .

Вывод. Если определитель, созданный из координат векторов $\overline{l}_{1}, \overline{l}_{2}, \overline{l}_{3}$ , не равен нулю, тогда эти векторы линейно независимы, то есть создают базис.

Теперь найдём координаты вектора $\overline{a}$ в базисе $\overline{l}_{1}, \overline{l}_{2}, \overline{l}_{3}$ , то есть найдём числа $\alpha, \beta, \gamma$ , такие, что выполняют равенство:

$\overline{a} = \alpha\overline{l}_{1} + \beta\overline{l}_{2} + \gamma\overline{l}_{3}$ .

Повторяя предыдущие преобразования, у нас получается:

$(9 - 9,5) = \alpha * (-1,4, -1) + \beta * (4, -1,1) + \gamma * (8, 1, 0) \to(-\alpha, 4\alpha, -\alpha) + (4\beta, -\beta, \beta) + (8\gamma, \gamma, 0) = 9, -9,5)\to(-\alpha + 4\beta + 8\gamma, 4\alpha - \beta + \gamma, -\alpha + \beta) = (9, -9,5).$

Приравнивая соответствующие координаты в левой и правой частях равенства, получим систему, которую удобно решать алгебраическим методом:

$\left\{ \begin{aligned} -\alpha + 4\beta + 8\gamma = 9\\ 4\alpha - \beta + \gamma = -9\\ -alpha + \beta = 5 \end{aligned} \right$

Таким образом, решив данную систему получим вектор $\overline{a} = -\overline{l}_{1} + 4\overline{l}_{2} - \overline{l}_{3}$

Добавить комментарий Отменить ответ

Лев Канеки на Как написать эссе – все правила от “А” до “Я”главное не зацикливаться и не падать в хандру или депрессию и всё будет хорошо
Татьяна на ПредпринимательствоБлагодарю вас! Очень полезная информация!
Фаррух на Как восстановиться в вузе после отчисленияСпасибо
влад на Более 50 основных формул по физике с пояснениемтут есть 8 ошибок в формулах
Илья на Метод Гаусса – теорема, примеры решенийбоже, сколько ошибок на сайте, посмотрите номер 3.