Геометрическое определение вероятности случайного события

О чем статья

Геометрическое определение вероятности

Рассмотрим, что такое геометрическая вероятность (геометрическое определение вероятности) на примерах некоторых задач. Пусть дан отрезок длиной $L$ . Разделим его пополам (для однозначности точку деления отнесём к левой половине). Наугад выкладывается точка на этот отрезок. Возможны два случая: «точка попала на левую половину» — событие $A_{1}$ ; «точка попала на правую половину» — событие $A_{2}$ . Так как точка кладётся наугад, тогда целесообразно считать, что эти события равновозможные. Тогда вероятность события $A_{1} = P(A_{1}) = 0.5$ , так же получается и с $A_{2} = P(A_{2}) = 0.5$ .

Теперь разделим отрезок $L$ на 10 равных частей (длина каждого $0.1 L$ ). Случайным образом бросаем точку на этот отрезок. Возможные случаи: «точка попала на первый отрезок» — событие $A_{1}$ , «точка попала на второй отрезок» — событие $A_{2}$ , «точка попала на третий отрезок» — событие $A_{3}$ и так до отрезка десятого — $A_{10}$ . Считая эти события равновозможными получаем, что вероятность каждого из этих событий равняется 0,1. То есть, $P(A_{i}) = 0.1$ $(i = \overline{1,10})$ .

Пусть событие $A$ заключается в том, что случайно брошенная точка попала, например на отрезок $[0.3 L : 0.7 L]$ . Так как событию $A$ способствуют четыре из возможных случаев, тогда вероятность можно представить:

$P(A) = 0,4 = {{0,4 L}\over{L}} = {1\over{L}}$ .

Отсюда следует:

$P(A) = {1\over{L}}$

(1)

— вероятность случайного попадания точки на отрезок длиной $l$ , который помещается на отрезке длиной $L (l\leq{L})$ .

Вышеизложенный подход можно обобщить для плоских фигур (см. рис. 1), а также в пространстве для тел.

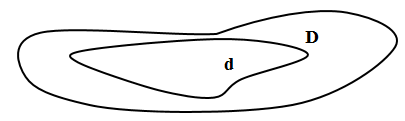
Геометрическая вероятность

Рис. 1

Пусть фигура $d$ , площадь которой равняется $s$ , помещается в фигуре $D (d\in{D})$ , площадь которой $S$ , тогда вероятность события $A$ , которое заключается в том, что наугад брошенная точка попадёт в фигуру $d$ , равняется отношению площади этих фигур, то есть:

$P(A) = {s\over{S}}$

(2)

Для формул (1) и (2) имеется ввиду «равновозможность» случайного попадания точки в произвольную точку отрезка $L$ или фигуры $D$ .

Геометрическая модель

С целью наглядности рассмотрим такую модель:

Пусть фигура $D$ — это прямоугольник размера $a$ x $b$ (его площадь $S = ab$ ), описанный вокруг фигуры $d$ , нарисованной на асфальте. Вместо точек, которые выбираются наугад в прямоугольнике, будем считать капли дождя, что только начинается. После определённого времени прямоугольник закроем от дождя и посчитаем количество капель $n$ , которые попали на весь прямоугольник $D$ , а также количество капель $m$ , которые попали на фигуру $d$ . Вычислим относительную частоту $M\over{n}$ . Нам уже известно что по формуле (2) можно найти вероятность событий $A$ , которое заключается в случайном выборе точки из фигуры $d$ . В данном случае это соотношение площадей $s\over{S}$ , а с другой стороны $P(A)\approx{m\over{n}}$ . Поэтому у нас получается приближённое равенство $s\over{S}\approx{m\over{n}}$ , при помощи которого можно найти площадь фигуры $d$ ,

$s\approx{m\over{n}}S$

(3)

Понятно, что этот пример приведён для наглядности, а в действительности лучше вычислять при помощи компьютерной программы. Однако, техника и не всегда может быть под рукой. Хотелось бы показать ещё несколько примеров, чтобы вы более ясно поняли тему геометрической вероятности.

Нужна помощь в написании работы?

Мы - биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Задачи по теме: «Геометрическое определение вероятности»

[stextbox id=»warning» caption=»Пример 1″]

Задача

Два студента после занятий договорились встретиться возле входа корпуса. Так как у каждого из них могли появиться непредвиденные обстоятельства, они договорились, что встреча состоится с 14.00 до 15.00. Таким образом, кто первый приходит к месту назначения, тот ждёт 15 минут (но не позже 15.00) и уходит. Найти вероятность встречи, если час ожидания взять:

а) 15 минут;

б) 20 минут;

в) 30 минут.

Решение

Пусть $x$ — час прихода первого студента на место встречи, $y$ — второго.

Встреча происходит при условии, что:

$|x - y|\leq{15}\to{-15}\leq{x - y}\leq{15}$ или

$\left\{ \begin{aligned} y\leq{x + 15}\\ y\geq{x - 15} \end{aligned} \right$

Множества решений неравенств изображено на рис. 2.

Площадь квадрата $S = 60^2 = 3600$ . Площадь фигуры $d$ .

$s = 3600 - (60 - t)^2$ . Поэтому вероятность встречи (событие $A$ ):

$P(A) = {s\over{S}} = {3600 - (60 - t)^2\over{3600}} = 1 - (1 - {t\over{60}})^2$ .

При $t = 15$ минут имеем $P(A)\approx{0,44}$ ;

при $t = 20$ минут: $P(A) = 0,55$ ;

при $t = 30$ минут: $P(A)\approx{0,75}$ .

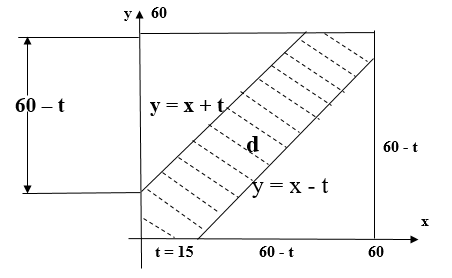
Геометрическое определение вероятности

Рис. 2

Ответ

Вероятность встречи при ожидании 15 минут приблизительно 0, 44;

Вероятность встречи при ожидании 20 минут = 0, 55;

Вероятность встречи при ожидании 30 минут около 0, 75.

[/stextbox]

[stextbox id=»warning» caption=»Пример 2″]

Задача

Найти площадь параболического сегмента, который задан равенствами:

1. $y = -x^2 + 4x$ ;

2. $y = 0$ .

Решение

Параболический сегмент показан на рис. 3.

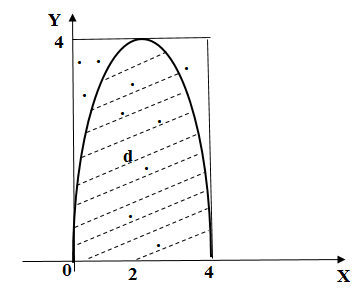
Геометрическое определение вероятности

Рис. 3

Точки пересечения с осью $OX$ — $x_{1} = 0$ и $x_{2} = 4$ .

Эту площадь можно вычислить при помощи определённого интеграла или при помощи формулы:

$s = {|a|(x_{2} - x_{1})^3\over{6}} = {|-1|(4 - 0)^3\over{6}} = {64\over{6}}\approx{10,667$ .

где $a$ — коэффициент при $x^2$ в равенстве параболы.

Покажем, как найти искомую площадь, используя геометрическое определение вероятности. Опишем вокруг параболического сегмента квадрат со стороной 4 единицы. Площадь квадрата $S = 16$ кв. ед. (см. рис. 3). При помощи стандартной функции генерирования случайных точек $n$ , которые попадают в квадрат, в том числе $m$ точек, которые в параболическом сегменте, найдём относительную частоту попадания случайных точек в параболический сегмент. Тогда по формуле (3) находим $s\approx{m\over{n}} * 16$ .

В таблице 1 даны результаты расчётов ближайших значений площади параболического сегмента для разных значений $m$ и $n$ . Так, из рис. 3 видно, что в квадрат попало 10 точек, а в сегмент — 6, поэтому первого приближения площади у нас получается:

$s = {6\over{10}} * 16 = {3\over{5}} * 16 = {48\over{5}} = 9,6$ ; что и записываем в первой строке табл. 1:

$n$	$m$	Площадь $s$
10	6	9,6
100	66	10,56
1 000	665	10,32
10 000	6 645	10,6336
100 000	66 865	10,6984
1000 000	666 727	10,6671

Таблица 1

Ответ

Площадь найдена при использовании геометрического определения вероятности, которая высчитана и записана в таблице.

[/stextbox]

Нашли ошибку? Выделите текст и нажмите CTRL + Enter

сагдиана на Решить уравнение с дробями онлайнничего не понятно!
акмарал на Более 50 основных формул по физике с пояснениема эти формулы обычно используют в олимпиядах
всем пока на Решить уравнение с дробями онлайнничего не понятно. калькулятор не работает.
Великий гей Никола Тесла на Более 50 основных формул по физике с пояснениемСайт параша, я пытался списать ЕГЭ по физике с помощью них, я блять сдал его на 99999 балов, и теперь
некто на Примеры решения матриц с ответамиНеправильные ответы, учите матрицу гении

Геометрическое определение вероятности случайного события