Giperbola: исследование ключевого математического понятия

О чем статья

Что такое гипербола

Гипербола – это множество точек плоскости, разница расстояний которых от двух заданных точек, фокусов, есть постоянная величина и равна $2a$ .

Аналогично эллипсу фокусы размещаем в точках $F_{1}(c, 0)$ , $F_{2}(-c, 0)$ (см. рис. 1).

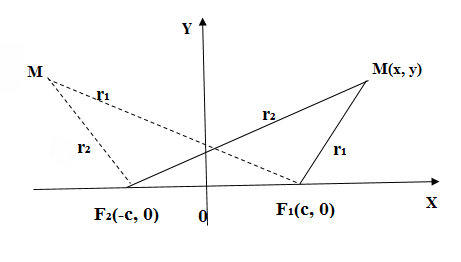
Изображение - гипербола

Рис. 1

Видно из рисунка, что могут быть случаи $r_{1} < r_{2}$ и $r_{1} > r_{2}$ , тогда согласно определению $r_{2} - r_{1} = \pm2a$

Известно, что в треугольнике разница двух сторон меньше третьей стороны, поэтому, например, с $\Delta{F_{2}}MF_{1}$ у нас получается:

$F_{2}M - F_{1}M < F_{1}F_{2}\to{r_{2} - r_{1}} < 2c\to{2a < 2c}\to{a < c}$ . Значит, для гиперболы $a < c$ .

Дальше запишем значение выражений $r_{1}$ и $r_{2}$ через координаты точек

$r_{2} = r_{1} \pm {2a}\to{\sqrt{(x + c)^2 + y^2}} = \sqrt{(x - c)^2 + y^2)}\pm2a$ .

Поднесём к квадрату обе части и после дальнейших преобразований найдём:

${x^2\over{a^2}} - {y^2\over{b^2}} = {1}$ .

(1)

где $b^2 = c^2 - a^2$ . Уравнение гиперболы (1) – это каноническое уравнение гиперболы.

Гипербола симметрична относительно координатных осей, поэтому, как и для эллипса, достаточно построить её график в первой четверти, где:

${y} = {b\over{a}}\sqrt{x^2 - a^2}$ . Область значения для первой четверти $a\leq{x} < {+\infty}$ .

При $x = a, y = 0$ у нас есть одна из вершин гиперболы $A_{1}(a, 0)$ . Вторая вершина $A_{2}(-a, 0)$ . Если $x = 0$ , тогда из (1) $-{y_{2}\over(b_{2}}) = 1$ – действительных корней нет. Говорят, что $B_{1}(0, b)$ и $B_{2}(0, -b)$ – мнимые вершины гиперболы. Из соотношением ${y} = {b\over{a}}{\sqrt{x^2 - a^2}}$ получается, что при достаточно больших значениях $x$ есть место ближайшего равенства ${b\over{a}}{\sqrt{x^2 - a^2}}\approx{b\over{a}}{\sqrt{x^2}} = {b\over{a}}x (x > a)$ . Поэтому прямая ${y} = {b\over{a}}x$ есть линией, расстояние между которой и соответствующей точкой гиперболы направляется к нулю при $x\to\infty$ .

Форма и характеристики гиперболы

Исследуем уравнение (1) форму и расположение гиперболы.

Переменные $x$ и $y$ входят в уравнение (1) в парных степенях. Поэтому, если точка $(x, y)$ принадлежит гиперболе, тогда и точки $(-x, y), (x, -y), (-x, -y)$ также принадлежат гиперболе. Значит, фигура симметрична относительно осей $OX$ и $OY$ , и точки $O(0, 0)$ , которая называется центром гиперболы.
Найдём точки пересечения с осями координат. Подставив в уравнение (1) $y = 0$ получим, что гипербола пересекает ось $OX$ в точках $A_{1}(a, 0), A_{2}(-a, 0)$ . Положив $x = 0$ получим уравнение $y^2 = -b^2$ , у которого нет решений. Значит, гипербола не пересекает ось $Oy$ . Точки $A_{1}, A_{2}$ называются вершинами гиперболы. Отрезок $A_{1}, A_{2}$ = $2a$ и называется действительной осью гиперболы, а отрезок $B_{1}, B_{2} = 2b$ – мнимой осью гиперболы. Числа $a$ и $b$ называются соответственно действительной и мнимой полуосями гиперболы. Прямоугольник, созданный осями $2a$ и $2b$ называется главным прямоугольником гиперболы.
С уравнения (1) получается, что ${x^2\over{a^2}}{\geq{1}}$ , то есть $|x|\geq{a}$ . Это означает, что все точки гиперболы расположены справа от прямой $x = a$ (правая ветвь гиперболы) и левая от прямой $x = -a$ (левая ветвь гиперболы).
Возьмём на гиперболе точку $(x, y)$ в первой четверти, то есть $x\geq{0}, y\geq{0}$ , а поэтому ${y} = {b\over{a}}{\sqrt{x^2 - a^2}}, {x\geq{a}}$ . Так как ${y'} = {bx\over{a\sqrt{x^2 - a^2}}} > 0$ , при $x > a$ , тогда функция монотонно возрастает при $x > a$ . Аналогично, так как ${y''} = -{ab\over{(x^2 - a^2)}}{^3\over{2}} < {0}$ при $x > a$ , тогда функция выпуклая вверх при $x > a$ .

Нужна помощь в написании работы?

Мы - биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Цена работы

Асимптоты гиперболы

Есть две асимптоты гиперболы. Найдём асимптоту к ветви гиперболы в первой четверти, а потом воспользуемся симметрией. Рассмотрим точку $x, y$ в первой четверти, то есть $x{\geq} 0, y{\geq} 0$ . В этом случае ${y} = {b\over{a}}\sqrt{x^2 - a^2}$ , $x\geq{a}$ , тогда асимптота имеет вид: $y = Kx + B$ , где

$K = {\lim\atop_{x\to +\infty}}}{y\over{x}}$ = ${\lim\atop_{x\to +\infty}}}$ x ${b\over{a}}{\sqrt{x^2 - a^2}}\over{x}$ = ${b}$ ,

$B = {\lim\atop_{x\to +\infty}}}(y(x) - Kx) = {\lim\atop_{x\to +\infty}}}({b\over{a}}\sqrt{x^2 - a^2} - {b\over{a}}x)$ = ${b\over{a}}{\lim\atop_{x\to +\infty}}$ x ${(\sqrt{x^2 - a^2} - x)}({\sqrt{x^2 - a^2} + x)}}\over{(x^2 - a^2} + x)$ = ${b\over{a}}{\lim\atop_{x\to +\infty}}$ x ${b^2\over{(\sqrt{x^2 - a^2)}} + x$ = ${0}$

Значит, прямая ${y} = {b\over{a}} = {x}$ – это асимптота функции ${y} = {b\over{a}}\sqrt{x^2 - a^2}, x\geq{a}$ . Поэтому в силу симметрии асимптотами гиперболы есть прямые $y = \pm{b\over{a}}x$ .

За установленными характеристиками построим ветвь гиперболы, которая находится в первой четверти и воспользуемся симметрией:

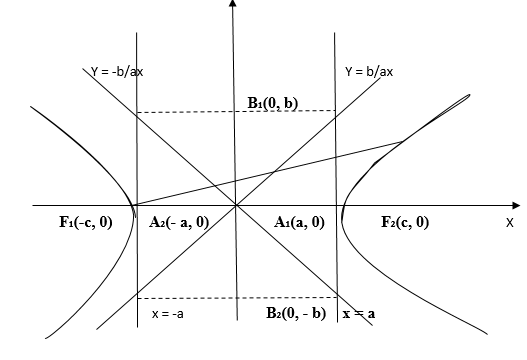
Уравнение гиперболы

Рис. 2

В случае, когда $b = a$ , то есть гипербола описывается уравнением $x^2 - y^2 = a^2$ . В этой гиперболе асимптоты, которые и есть биссектрисами координатных углов $y = \pm{x}$ .

Примеры задач на построение гиперболы

[stextbox id=”warning” caption=”Пример 1″]

Задача

Найти оси, вершины, фокусы, ексцентриситет и уравнения асимптот гиперболы. Построить гиперболу и её асимптоты.

$9x^2 - 16y^2 - 144 = 0$

Решение

Сведём уравнение гиперболы к каноническому виду:

$9x^2 - 16y^2 - 144 = 0\to{9x^2 - 16y^2 = 144\arrowvert{:}144\to{x^2\over{16}} - {y^2\over{9}} = {1}$ .

Сравнивая данное уравнение с каноническим (1) находим $a^ = 16$ , $b^2 = 9$ , $c^2 = 16 + 9 = 25\to{2a = 8, 2b = 6, 2c = 10}$ . Вершины $A_{1}(4, 0), A_{2}(-4, 0)$ , фокусы $F_{1}(5, 0)$ и $F_{2}(-5, 0)$ . Ексцентриситет $\varepsilon = {5\over{4}} = {1, 25}$ ; асмптоты $y = \pm{3\over{4}}x$ ; Строим параболу. (см. рис. 3)

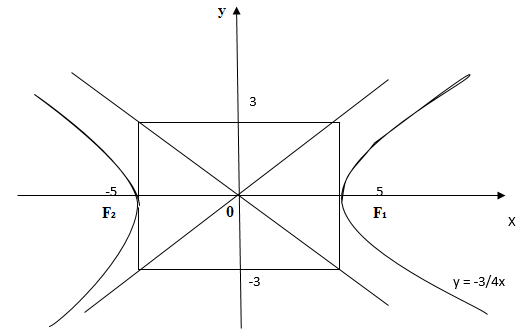
Построение гиперболы

Рис. 3

[/stextbox]

[stextbox id=”warning” caption=”Пример 2″]

Задача

Даны фокусы гиперболы $F_{1}(-10, 0), F_{2}(10, 0)$ и её асимптота $4x + 3y = 0$ . Написать уравнение гиперболы:

Решение

Записав уравнение асимптоты в виде $y = -{4\over{3}}x$ находим отношение полуосей гиперболы ${b\over{a}} = {4\over{3}}$ . По условию задачи следует, что $c = 10$ . Поэтому $a^2 + b^2 = 100$ Задачу свели к решению системы уравнений:

$\left\{ \begin{aligned}{b\over{a}} = {4\over{3}}\\a^2 + b^2 = 100\end{aligned}\right$

Подставляя ${b} = {4\over{3}}a$ во второе уравнение системы, у нас получится:

${a^2} + {16a^2\over{9}} = 100$ ,

откуда $a^2 = 36$ . Теперь находим $b^2 = ({4\over{3}}a)^2 = {16\over{9}} * 36 = 64$ .

Следовательно, у гиперболы получается такое уравнение:

${x^2\over{36}} - {y^2\over{64}} = {1}$ .

Ответ

Уравнение гиперболы ${x^2\over{36}} - {y^2\over{64}} = {1}$ .