О чем статья

Что такое множество чисел

Определение

Термин множества чисел можно описать, как совокупность, объединение, набор некоторых объектов произвольной природы – элементы множества. Например, множество книг в библиотеке, множество студентов факультета, множество парных чисел, множество точек заданного отрезка и т. п.

Если элемент $x$ принадлежит множеству $A$ , тогда пишут $x\in{A}$ , если же элемент $y$ не принадлежит множеству $A$ , тогда пишут, что $y\notin{A}$ или $y\overline\in{A}$ .

Множества, в которых нет ни одного элемента, называется пустым множеством и обозначается $\varnothing$ .

Рассмотрим несколько важных операций:

1. Два множества $A$ и $B$ называются равными (обозначают $A = B$ ), если они состоят из одинаковых элементов.

2. Множество $A$ называется подмножным множеством $B$ , если каждый элемент множества $A$ есть элементом множества $B$ .

Это обозначается так: $A\subset{B}$ и читается $A$ содержится в $B$ или в $B$ находится $A$ . Очевидно, что пустое множество входит в любое множество $A: \varnothing\subset A$ .

Например, если множество $A$ состоит из элементов $1, 2, 3, 4, 5, 6, 7$ обозначают:

$A$ = { $1, 2, 3, 4, 5, 6, 7$ }), а в $B$ = { $2, 3, 5, 7$ } тогда $B\subset{A}$ .

3. Множества элементов $C$ , которые принадлежат множеству $A$ или множеству $B$ , или $A$ и $B$ , называется объединением этих множеств и обозначается $C = A\cup{B}$ .

4. Множества элементов $C$ , которые принадлежат двум множествам $A$ и $B$ называется пересечением множеств $A$ и $B$ и обозначается $C = A\cap{B}$

Если, например, $A$ и $B$ – это множества точек, что принадлежат двум фигурам соответственно, тогда схематически на рис. 1 изображены их объединения в случаях а) и б). На рис. 2 изображено пересечение множеств $A$ и $B$ .

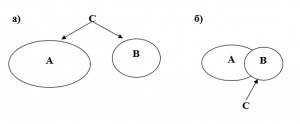
Множества чисел

Рис. 1

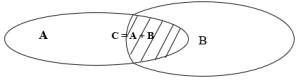
Элементы множества

Рис. 2

5. Разницей множеств A и $B$ называется множество $C = A \ B$ , что содержит те элементы $A$ , которые не есть элементами множества $B$ (см. рис. 3).

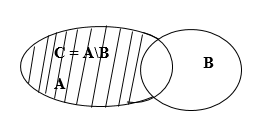
Множества чисел

Рис. 3

Виды чисел

Существует 7 видов чисел:

1. Натуральные – $N$ ;

2. натуральные числа, в которые включается нуль – $N_{0}$ ;

3. целые числа – $Z$ ;

а) целые положительные числа – $Z^{+}$ ;

б) целые отрицательные числа – $Z^{-}$ ;

4. рациональные числа – $Q$ ;

5. иррациональные числа

6. Действительные числа – $R$ ;

7. Комплексные числа – $C$ .

Рассмотрим каждый вид числа более подробно:

1. Натуральные числа всегда используются при естественном счёте или перечислении предметов, вернее при их нумерации, то есть “первый”, “второй”, “третий”. Описывается множество натуральных чисел так:

$N$ = {1, 2, 3, …, }.

2. Натуральные числа, в которые включён нуль используются для обозначения количества предметов:

$N$ = {0, 1, 2, 3, …}

3. Целые числа – это числа, в которые входят натуральные числа с положительным и отрицательным знаками:

а) целые положительные числа (обозначаются $Z^{+}$ ) и пишутся: $Z^{+} = N =$ {1, 2, 3, …};

б) целые отрицательные числа (обозначаются $Z^{-}$ ) и пишутся: $Z^{-} = N$ {…, -3, -2, -1};

$Z = Z^{-}\cup {0}\cup{Z^{+}}$ = {…, -3, -2, -1, 0, 1, 2, 3, …}.

4. Рациональные числа – числа, которые представляются в виде обыкновенной дроби $m/n$ , где $m$ и $n$ – целые числа, а $n\neq{0}$ . Рациональные числа обозначаются латинской большой буквой $Q$ :

$Q$ = { $x | x = m/n, m\in{Z}, n\in{Z}, n\neq{0}$ }. Если переводить в десятичную дробь, тогда рациональное число может представляться конечной и бесконечной дробью.

5. Иррациональные числа – вещественное число, которое не рациональное и не может представляться в виде десятичной дроби.

6 Действительные числа или вещественные – это числа, в которых объединяются рациональные и иррациональные числа ( $R$ ).

7. Комплексные числа – это числа, в которых содержится $i$ – мнимая единица:

$C$ = { $x + iy | x\in{R}$ и $y\in{R}$ }.

Нужна помощь в написании работы?

Мы - биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Цена работы

Примеры решения задач

Пример 1

Задача

Записать множество $E$ , если $E = A\cup{B}$ , причём $A$ = {2, 4, 6, 8, 10, 12}, $B$ = {3, 6, 9, 12}.

Решение

$E = A\cup{B}$ есть не что иное, как объединение множеств $A$ и $B$ , то есть, множество $E$ будет состоять из элементов, принадлежащих как множеству $A$ , так и множеству $B$ : $E$ = {2, 3, 4, 6, 8, 9, 10, 12}.

Ответ

Множество $E$ состоит из элементов, которые принадлежат двум множествам $A$ и $B$ .

Пример 2

Задача

Все студенты курса изучают разные иностранные языки. Значит, из них, 91 студент изучает английский язык, ещё 96 студентов изучают немецкий язык, 94 студента изучают исключительно французский язык, 36 студентов изучают не только английский, но и немецкий языки, ещё 32 студента изучают английский и французский языки, а 10 студентов занимаются изучением всех языков без исключения.

Вопрос: сколько студентов занимаются изучением немецкого и французского языков, если всего на курсе по списку 189 студентов?

Решение

Итак, для начала введём обозначения:

$A$ – множество всех студентов, которые находятся на данном курсе;

$A_{1}$ – множество студентов, которые изучают только английский язык;

$A_{2}$ – множество студентов, которые занимаются изучением немецкого языка;

$A_{3}$ – множество студентов, изучающих исключительно французский язык;

$A_{12}$ – множество студентов, которые изучают, как английский, так и немецкий язык;

$A_{13}$ – множество студентов, изучающие английский и французский языки;

$A_{23}$ – множество студентов, которіе изучают немецкий и французский язіки;

$A_{123}$ – множество студентов, которые изучают абсолютно все языки;

$|B|$ – количество элементов множества $B$ .

По условию задачи:

$|A| = 189, |A_{1}| = 91, |A_{3}| = 94, |A_{12}| = 36, |A_{23}| = 32, |A_{23}| = x.$

Найдём $x$ – количество студентов, которые изучают немецкий и французский языки. Согласно вышеописанному обозначению, у нас получается:

$A_{12} = A_{1}\cup{A_{2}}$ , $A_{13} = A_{1}\cup{A_{3}}$ , $A_{23} = A_{2}\cup{A_{3}}$ , $A_{123} = A_{1}\cup{A_2}\cup{A_{3}}$ .

Из методов включения и исключения следует, что

$|A| = |A_{1}| + |A_{2}| + |A_{3}}| - |A_{1}\cup{A_{2}}| - |A_{1}\cup{A_{3}}| - |A_{2}\cup{A_{3}}| - |A_{1}\cup{A_{2}}\cup{A_{3}}| =\\ = |A_{1}| + |A_{2}| + |A_{3}| - |A_{12}| - |A_{13}| - |A_{23} + A_{123}|$ .

$189 = 91 + 96 + 94 - 36 - 32 - x + 10 189 = 223 - x x = 223 - 189 = 34$

Ответ

$34$ студента занимаются изучением немецкого и французского языков.

Нашли ошибку? Выделите текст и нажмите CRTL + Enter

Филипп Х.

Редактор.

Копирайтер, коммерческий автор, писатель, сценарист и автор-универсал в широком смысле.

Добавить комментарий Отменить ответ

Den777 на Компьютерное тестирование: основы, методы и преимущества в современном миреЛучшей же программой тестирования для проверки знаний людей является - Indigo.
Игорь на Искусственный интеллект и робототехника: как они взаимодействуют и влияют друг на другаЕсть третий вариант: Пиар этой отрасли ради её дальнейшего финансирования преувеличивает возможности ИИ в конструктивной сфере. ИИ не обладает реальным
Игорь на Кибернетика и теория эволюции: взаимосвязь, принципы и моделированиеПредлагаю ознакомиться с несколько иным взглядом на отношения кибернетики и теории эволюции. Это статья "Синтез структуры организованных систем как центральная
АЛЕКСЕЙ РЫБАКОВ на Искусственный интеллект и робототехника: как они взаимодействуют и влияют друг на другаДавно в интернете задаю вопрос и не получаю ответа : Учёные бьются над созданием роботов копирующих людей . (проблемы ,
Торгын на Язык газеты: особенности и стиль в сравнении с другими СМИСпасибо, очень полезная статья, спасибо автору.

Множества чисел и примеры числовых множеств

Что такое множество чисел

Виды чисел

Примеры решения задач