О чем статья
Введение
Приветствую вас, дорогие студенты! Сегодня мы начнем изучение одной из самых важных и широко применяемых тем в теории вероятности – нормального распределения. Нормальное распределение является одним из основных распределений вероятностей и широко используется в различных областях, таких как статистика, физика, экономика и многие другие.
Нужна помощь в написании работы?

Мы - биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Определение нормального распределения
Нормальное распределение, также известное как гауссово распределение, является одним из наиболее важных и широко используемых распределений в теории вероятности и статистике. Оно характеризуется своей симметричной формой и колоколообразным графиком.
Нормальное распределение определяется двумя параметрами: средним значением (μ) и стандартным отклонением (σ). Среднее значение определяет центр распределения, а стандартное отклонение определяет его разброс.
Функция плотности вероятности нормального распределения имеет следующий вид:
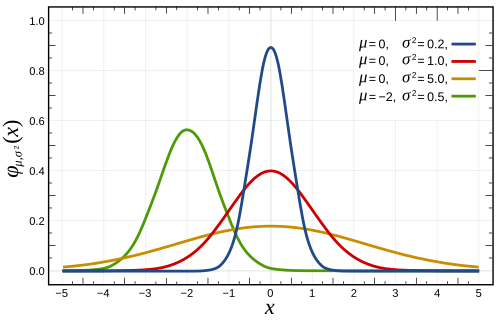
График функции плотности вероятности нормального распределения имеет форму колокола, симметричную относительно среднего значения. Вероятность попадания случайной величины в определенный интервал определяется площадью под графиком функции плотности вероятности в этом интервале.
Нормальное распределение имеет несколько важных свойств:
- Сумма или среднее значение независимых нормально распределенных случайных величин также будет иметь нормальное распределение.
- Линейная комбинация нормально распределенных случайных величин также будет иметь нормальное распределение.
- Центральная предельная теорема утверждает, что сумма большого числа независимых случайных величин, каждая из которых имеет одно и то же распределение, будет приближаться к нормальному распределению.
Свойства нормального распределения
Нормальное распределение, также известное как распределение Гаусса, является одним из наиболее важных и широко используемых распределений в статистике и теории вероятностей. Оно имеет несколько свойств, которые делают его особенно полезным для моделирования случайных явлений.
Симметричность
Нормальное распределение симметрично относительно своего среднего значения. Это означает, что вероятность того, что случайная величина примет значение меньше среднего, равна вероятности того, что она примет значение больше среднего.
Однозначность
Нормальное распределение полностью определяется двумя параметрами: средним значением (μ) и стандартным отклонением (σ). Среднее значение определяет центр распределения, а стандартное отклонение определяет его разброс. Это означает, что если мы знаем эти два параметра, мы можем полностью описать форму нормального распределения.
Кривая колокола
Нормальное распределение имеет форму кривой колокола, симметричной относительно своего среднего значения. Это означает, что большинство значений случайной величины будут близки к среднему значению, а значения, находящиеся далеко от среднего, будут встречаться реже.
Плотность вероятности
Функция плотности вероятности нормального распределения имеет гладкую и симметричную форму. Она достигает максимума в среднем значении и убывает по мере удаления от него. Плотность вероятности определяет вероятность того, что случайная величина примет определенное значение или попадет в определенный интервал значений.
Центральная предельная теорема
Нормальное распределение играет важную роль в центральной предельной теореме. Согласно этой теореме, сумма большого числа независимых случайных величин, каждая из которых имеет одно и то же распределение, будет приближаться к нормальному распределению. Это свойство делает нормальное распределение особенно полезным для анализа данных и статистических выводов.
Стандартное нормальное распределение
Стандартное нормальное распределение – это особый вид нормального распределения, который имеет среднее значение равное нулю и стандартное отклонение равное единице. Оно также называется стандартизированным нормальным распределением.
Стандартное нормальное распределение обозначается буквой Z и используется для стандартизации других нормальных распределений. Стандартизация позволяет сравнивать значения из разных нормальных распределений и делать статистические выводы.
Функция плотности вероятности стандартного нормального распределения имеет форму колокола и симметрична относительно нуля. Она достигает максимума в точке нуль и убывает по обе стороны. Площадь под кривой функции плотности вероятности равна единице, что означает, что вероятность любого значения в стандартном нормальном распределении равна 1.
Стандартное нормальное распределение играет важную роль в статистике и теории вероятности. Оно используется для вычисления вероятностей, построения доверительных интервалов, проверки гипотез и других статистических задач. Также оно является основой для многих статистических методов и моделей.
Формула плотности вероятности нормального распределения
Нормальное распределение, также известное как гауссовское распределение, является одним из наиболее распространенных и важных распределений в статистике и теории вероятности. Оно характеризуется своей симметричностью и колоколообразной формой.
Формула плотности вероятности нормального распределения имеет следующий вид:
f(x) = (1 / (σ * √(2π))) * e^(-((x – μ)^2 / (2σ^2)))
где:
- f(x) – плотность вероятности для значения x
- μ – математическое ожидание (среднее значение) распределения
- σ – стандартное отклонение распределения
- e – основание натурального логарифма (приближенное значение 2.71828)
- π – число пи (приближенное значение 3.14159)
Формула позволяет вычислить вероятность того, что случайная величина x примет определенное значение в нормальном распределении. Плотность вероятности определяет, насколько вероятно появление конкретного значения в данном распределении.
Нормальное распределение имеет много свойств и применений в различных областях, таких как физика, экономика, биология и другие. Оно является основой для многих статистических методов и моделей, и его понимание является важным для студентов, изучающих теорию вероятности и статистику.
Центральная предельная теорема и нормальное распределение
Центральная предельная теорема (ЦПТ) является одной из основных теорем теории вероятности. Она утверждает, что сумма большого числа независимых и одинаково распределенных случайных величин стремится к нормальному распределению, независимо от их исходного распределения.
ЦПТ имеет большое практическое значение, так как позволяет использовать нормальное распределение для аппроксимации распределения суммы случайных величин, даже если исходные величины не имеют нормального распределения.
Формально, ЦПТ утверждает следующее:
Формулировка ЦПТ
Пусть X1, X2, …, Xn – независимые и одинаково распределенные случайные величины с конечным математическим ожиданием μ и дисперсией σ2. Тогда сумма Sn = X1 + X2 + … + Xn стремится к нормальному распределению с математическим ожиданием nμ и дисперсией nσ2 при n, стремящемся к бесконечности.
То есть, при достаточно большом n, распределение суммы случайных величин становится все более и более похожим на нормальное распределение.
Нормальное распределение имеет много полезных свойств, которые делают его удобным для анализа данных и построения статистических моделей. Оно симметрично относительно своего математического ожидания, имеет колоколообразную форму и хорошо описывает многие естественные явления.
ЦПТ и нормальное распределение широко используются в статистике для оценки параметров, проверки гипотез, построения доверительных интервалов и других статистических процедур. Поэтому понимание ЦПТ и нормального распределения является важным для студентов, изучающих теорию вероятности и статистику.
Сравнительная таблица нормального распределения
| Свойство | Определение | Пример |
|---|---|---|
| Симметричность | Распределение симметрично относительно своего среднего значения | Нормальное распределение с математическим ожиданием 0 |
| Однородность | Распределение имеет одинаковую дисперсию во всех своих точках | Нормальное распределение с дисперсией 1 |
| Центральная предельная теорема | Сумма большого числа независимых случайных величин имеет распределение, близкое к нормальному | Сумма 1000 бросков монеты |
| Формула плотности вероятности | Функция, описывающая вероятность попадания случайной величины в определенный интервал | Формула плотности вероятности нормального распределения |
Заключение
Нормальное распределение является одним из наиболее важных и широко используемых распределений в теории вероятности. Оно характеризуется симметричной формой и позволяет описывать множество случайных явлений в природе и обществе. Свойства нормального распределения, такие как среднее значение и стандартное отклонение, позволяют нам анализировать и предсказывать вероятности различных событий. Стандартное нормальное распределение, которое имеет среднее значение равное нулю и стандартное отклонение равное единице, играет особую роль в статистике и позволяет нам стандартизировать и сравнивать различные значения. Формула плотности вероятности нормального распределения позволяет нам вычислять вероятности для различных интервалов значений. Центральная предельная теорема показывает, что сумма большого числа независимых и одинаково распределенных случайных величин стремится к нормальному распределению, что делает его еще более полезным в практических приложениях. В целом, понимание нормального распределения является важным инструментом для анализа данных и принятия решений в различных областях науки и бизнеса.
