Постоянные и переменные величины

Существуют постоянные и переменные величины. Постоянные – это те величины, которые при заданном условии не меняют своего значения. Переменными величинами называются тогда, когда приобретаются разные значения.

Елена

10 июля 2017 0 7908

О чем статья

Постоянная величина

Определение

Постоянная величина – это величина, которая при заданных условиях не меняет своего значения.

Чтобы убедиться, что постоянная величина существует, вспомним несколько известных примеров: отношение длины круга к диаметру, как известно, равняется $\pi = 3,1415...$ ; сумма внутренних углов треугольника равна $180^0$ ; черырехугольника – $360^0$ ; скорость света в вакууме $C = 299 800$ км/с, постоянным есть ускорение земного притяжения в данной точке Земли и т. п.

Постоянная величина обозначается начальными буквами латинского алфавита – $a, b, c$ .

Нужна помощь в написании работы?

Мы - биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Переменная величина

Определение

Переменная величина – это величина, которая в данном процессе приобретает разные значения.

Рассмотрим переменную величину на примере: в процессе движения точки переменными есть пройденный точкой путь, её координаты, относительно заданной системы координат и т. п.

Переменная величина записывается последними буквами латинского алфавита – $x, y, z$ . Среди переменных величин удобно выделить такие, что приобретают отдельные изолированные значения, например, значение натуральных чисел $n = 1, 2, 3,...$ , или значения некоторой последовательности, например, арифметической или геометрической прогрессий. Такие переменные принято обозначать $x_n$ и называть дискретными переменными.

Если переменная величина приобретает все значения с некоторого промежутка, тогда считают, что она меняется непрерывно. Например, длина столбика термометра при перемене температуры принимает все значения с некоторого отрезка. Посмотрите ниже, как это выглядит на примере.

Пусть $a$ и $b$ – действительные числа, $a < b$ , им отвечают точки на числовой оси.

Отрезком $[a,b]$ называется множество чисел (точек) $x$ что удовлетворяют условия $a\leq{x}\leq{b}$ , при этом пишут ещё $x\in{[a, b]$ .

Интервалом $(a, b)$ называется множества чисел $x$ , что удовлетворяют условия $a < x < b$ . Множество всех действительных чисел (точек числовой прямой) будем обозначать интервалом $(-\infty; +\infty)$ , это означает, что для переменной $x$ выполняется неравность $-\infty < x < +\infty$ . Интервал $(a, +\infty)$ – это множество чисел, которые больше $a$ , или множество чисел, что удовлетворяют неравности $a < x < +\infty$ Аналогично интервал $(-\infty, b)$ означает множеству точек $x$ таких, что $-\infty < x < b\longleftrightarrow{x}\in{(-\infty, b)}$ .

Полуинтервалами $[a, b)$ или $(a, b]$ называется множество точек, для которых соответственно $a\leq{x} < {b}$ или $a < x \leq{b{$ .

Отрезок, интервал или полуинтервал мы будем называть ещё промежутком. Промежутки перемены переменной $x$ могут появляться, например, при решении неравенств, которые в свою очередь появляются при исследовании функции.

Примеры решений по теме : “Постоянные и переменные величины”

Пример 1

Задача

Определить промежутки перемены переменной $x$ , которые заданы неравенством: $3x + 5 > 0$ ;

Решение

1. $3x + 5 > 0\to{3x > -5}\to{-{5\over{3}}}$ или $-{5\over{3}} < x$ .

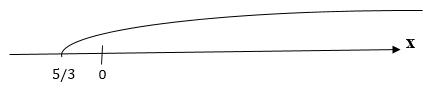
Переменная величина

Ответ

Область решений – промежуток: $-1{2\over{3}} < x < +\infty$ .

Пример 2

Задача

Определить промежутки перемены переменной $x$ , которые заданы неравенством: $x^2 \leq {9}$

Решение

$x^2 \leq {9}\to{x^2} - 9\leq{0}\to{(x + 3)(x - 3) \leq{0}$ .

Неравенство решается методом интервалов, определяя знак выражения $(x + 3)(x - 3)$ в “пробных” точках каждого из интервалов.

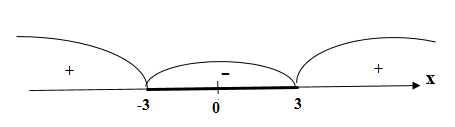
Постоянная величина

Ответ

Область решений – отрезок $-3 \leq {x} \leq {3}$ или $[-3, 3]$ .

Пример 3

Задача

Определить промежутки перемены переменной $x$ , которые заданы неравностью: $-7 <5 - 2x \leq{9}$

Решение

Для решения двойного неравенства отнимем из всех её частей по 5 и разделим на (-2) (при делении знаки неравенств меняются с отрицательного числа на противоположное).

$-7 - 5 < 5 - 2x - 5 \leq {9 - 5}\to{ -|2 < -2x \leq{4}}|: (-2) \to {6} > x \geq {-2}$ или $-2 \leq{x} < 6$ , или же $x\in[-2; 6)$ .

Переменная величина

Ответ

$6 > x \geq {-2}$ или $-2 \leq{x} < 6$ , или же $x\in[-2; 6)$ . Из них любой ответ считается верным.

. на ТОП-14 видов шпаргалок на экзамен и зачет (палим тему)Гениально! Спасибо огромное! Скажу результат, когда напишу контрольную по истории)
Алиса на Как отчислиться из вуза по собственному желаниюКак быть если отчислиться в конце ноября, если у тебя заочное обучение
Дима на Как решить задачу по математикеЗа 94000руб и куплена холодильник кахане кухонный гарнитур плита из стол плита на 12000₽ дешевле кухонного к эээ Пока гарнитура
Тагир на ПредпринимательствоСпасибо за оценку:)
Greg на ПредпринимательствоСпасибо за статью! Очень помогла!) А то столько просмотров, а никто даже не напишет "спасибо".