Угол между векторами
Рассмотрим, как получается угол между векторами. Пусть заданы ненулевые векторы 
и 
. Соединим эти векторы с общей точкой 
и в направлениях векторов и проведём с точки лучи (см. рис. 1)
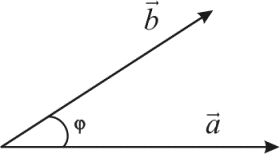
Рис. 1
и и обозначается так: 
^
Угол между вектором и нулевым вектором не обозначается.
Очевидно, что если 
, тогда ^
= 
. Если же 
, тогда 
^ = 
.
Нужна помощь в написании работы?
Мы - биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Примеры нахождения угла между векторами
В теме разобрались и теперь осталось закрепить её при помощи нескольких примеров.
Найти угол между векторами = 
и = 
Решение:
Для начала нужно найти скалярное произведение векторов:
x = 
+ 
x 
= 
Следующий шаг – найти модуль вектора:
= 
= 
= 
= 
= 
= 
= =
Теперь находим угол между векторами:
= 
= 
= 
= 
= 
Найти угол между векторами 
и 
Решение:
Находим модели векторов:
Находим угол между векторами:
= = 
= 