Векторное произведение

Векторное произведение двух векторов a и b – это вектор, который перпендикулярен плоскости этих же обоим исходным векторам.

Что такое векторное произведение векторов

[stextbox id=»info» defcaption=»true»]Векторное произведение векторов $\overline{a}$ и $\overline{b}$ называется вектор $\overline{c}$ = $\overline{a}$ x $\overline{b}$ , который удовлетворяет условия:

1). $\overline{c}\perp\overline{a}$ , $\overline{c}\perp\overline{b}$ , $\overline{c}$ — перпендикулярный плоскости векторов $\overline{a}$ и $\overline{b}$ ;

2). $\overline{|c|}$ = $\overline{|a|}$ x $\overline{|b|}$ x $sin(\overline{a}$ ^ $\overline{b})$ — модуль вектора $\overline{c}$ численно равен площади плоскости параллелограмма, построенного на векторах $\overline{a}$ и $\overline{b}$ ;

3).вектор $\overline{c}$ направлен в ту сторону, от которого поворот от $\overline{a}$ к $\overline{b}$ на наименьший угол осуществляется против часовой стрелки.[/stextbox]

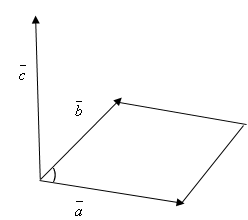
Изображение векторного произведения

Рис. 1

Алгебраические свойства векторного произведения

Давайте рассмотрим свойства векторного произведения.

Если $\overline{a}, \overline{b}, \overline{c}$ — произвольные векторы, а $\lambda$ — произвольные число, тогда:

$\overline{a}$ x $\overline{b}$ = $-\overline{b}$ x $\overline{a}$ . (Векторное произведение антикоммутативно).
$(\lambda\overline{a})$ x $\overline{b}$ = $\overline{a}$ x $(\lambda\overline{b})$ = $\lambda(\overline{a}$ x $\overline{b})$ .(Векторное произведение обладает сочетательным свойством относительно скалярного множителя).
$(\overline{a} + \overline{b})$ x $\overline{c}$ = $\overline{a}$ x $\overline{c}$ + $\overline{b}$ x $\overline{c}$ .
$\overline{a}$ x $\overline{b}$ = $0 \Longleftrightarrow(\overline{a}$ || $\overline{b})$ , $\overline{a}\neq{0}$ , $\overline{b}\neq{0}$ . (Два ненулевых вектора коллинеарны только тогда, когда их векторное произведение равно нулевому вектору).

Таблица векторного умножения ортов

$\overline{i}$ x $\overline{j}$ = $\overline{k}$ , $\overline{j}$ x $\overline{i}$ = $-\overline{k}$ ;

$\overline{j}$ x $\overline{k}$ = $\overline{i}$ , $\overline{k}$ x $\overline{j}$ = $-\overline{i}$ ;

$\overline{k}$ x $\overline{i}$ = $\overline{j}$ , $\overline{i}$ x $\overline{k}$ = $-\overline{j}$ .

$\overline{i}$ x $\overline{i}$ = $\overline{j}$ x $\overline{j}$ = $\overline{k}$ x $\overline{k}$ = $\overline{0}$ .

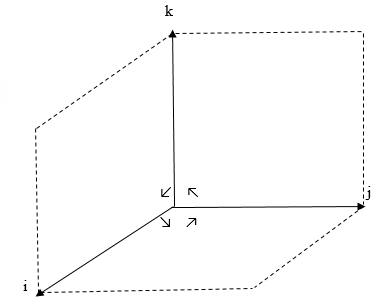
Векторное произведение ортов.

Рис. 2

Векторное произведение одноимённых ортов равняется $\overline{0}$ . При самом коротком повороте от одного орта к другому против часовой стрелки получаем третий орт, а по часовой стрелке – третий орт со знаком $``-``$ .

Формулы векторного произведения в координатной форме

Формулы векторного произведения в координатной форме получаем с учётом таблицы векторного произведения ортов:

$\overline{a}$ x $\overline{b}$ = $(x_{1}\overline{i} + y_{1}\overline{j} + z_{1}\overline{k})$ x $(x_{2}\overline{i} + y_{2}\overline{j} + z_{2}\overline{k})$ = $(y_{1}z_{2} - y_{2}z_{1})$ x $\overline{i} - (x_{1}z_{2} - x_{2}z_{1})$ x $\overline{j} + (x_{1}y_{2} - x_2y_1)$ x $\overline{k}$ =

$\begin{vmatrix} y_{1}&z_{1}\\ y_{2}&z_{2} \end{vmatrix}$ x $\overline{i}$ – $\begin{vmatrix} x_{1}&z_{1}\\ x_{2}&z_{2}\end{vmatrix}$ x $\overline{j}$ + $\begin{vmatrix} x_{1}&y_{1}\\ x_{2}&y_{2} \end{vmatrix}$ x $\overline{k}\Longleftrightarrow\overline{a}$ x $\overline{b}$ = $\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\x_{1}&y_{1}&z_{1}\\x_{2}&y_{2}&z_{2} \end{vmatrix} \right$

Примеры нахождения векторного произведения

Чтобы закрепить материал, рассмотрим на примерах, как найти векторное произведение векторов.

[stextbox id=»warning» caption=»Пример 1″]

Найти векторное произведение векторов $\overline{a}$ = $(1, 3, -1)$ и $\overline{b}$ = $(0, 2, 1)$ . Построить в системе координат векторы $\overline{a}, \overline{b}$ и $\overline{c}$ = $\overline{a}$ x $\overline{b}$ .

Решение:

Обратите внимание, что определитель (1) удобнее вычислять, если применить теорему про разложение за элементами первой строки:

$\overline{c}$ = $\overline{a}$ x $\overline{b}$ = $\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\ 1&3&-1\\ 0&2&1 \end{vmatrix}$ = $\overline{i}\begin{vmatrix} 3&-1\\ 2&1 \end{vmatrix}$ — $\overline{j}\begin{vmatrix} 1&-1\\ 0&1 \end{vmatrix}$ + $\overline{k}\begin{vmatrix} 1&3\\ 0&2 \end{vmatrix}$ = $5\overline{i} - \overline{j} + 2\overline{k} = (5, -1, 2).$

Теперь построим векторы $\overline{a}, \overline{c},\overline{b}$ по их координатам.

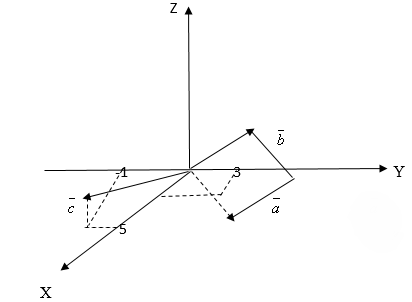
Как найти векторное произведение

Рис. 3

Из рисунка видно, что положение найденного вектора $\overline{c}$ отвечает определению векторного произведения $\overline{a}$ x $\overline{b}$ .

[/stextbox]

[stextbox id=»warning» caption=»Пример 2″]

Найти площадь треугольника $A, B, C$ , если $A(1, 2, -1), B(2, 3, 1), C(0, 1, 4)$ .

Решение:

Сначала находим векторы:

$\overline{AB} = (1, 5, 2)$ и $\overline{AC} = (-1, 3, 5)$ и их векторное произведение:

$\overline{AB}$ x $\overline{AC}$ = $\begin{vmatrix} \overline{i}&\overline{j}&\overline{k}\\ 1&5&2\\ -1&3&5 \end{vmatrix}$ = $19\overline{i} - 7\overline{j} + 8\overline{k}$ .

Длина полученного вектора по определению численно равняется площади параллелограмма, построенного на данных векторах и поэтому:

$S$ пар = $|\overline{AB}$ x $\overline{BC}|$ = $\sqrt{19^2 + (-7)^2 + 8^2}$ = $\sqrt{472}\approx21,77$ .

А площадь треугольника $A, B, C$ составляет половину найденной площади, то есть:

$S$ тр. = $1\over{2}$ $S$ пар = $1\over{2}$ x $\sqrt{472}\approx$ $1\over{2}$ x $21,77\approx10,89$ ,