Проекция вектора на ось и свойства проекции

Проекция вектора (допустим, a) на ось L – это разность X1 – X2 между координатами проекций конца и начала вектора на эту же ось.

Определение и свойства проекции

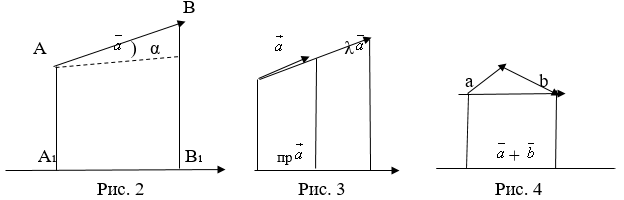
[stextbox id=”info” defcaption=”true”]Проекция вектора на ось (вектор – $\overline{a}$ , ось $l$ – обозначается $pr_l\overline{a}$ ) называется длина отрезка, которая соединяет проекции на эту ось начала и конца вектора, взята со знаком $(+)$ , если угол между вектором и осью острый и со знаком $(-)$ , если этот угол тупой (см. рис. 2). [/stextbox]

Очевидно, что когда $\overline{a}$ перпендикулярна $\overline{l}$ , тогда $pr_l\overline{a} = 0$ , и наоборот.

Основные свойства проекций:

1). $pr_l\overline{a}$ = $|\overline{a}|cos(a$ ,^ $\overline{l})$ (рис. 2);

2). $pr_l(\lambda\overline{a})$ = $\lambda{pr_l}\overline{a}$ (рис. 3);

3). $pr_l(\overline{a} + \overline{b})$ = $pr_l\overline{a}$ + $pr_l\overline{b}$ (рис. 4).

Свойство 3 выполняется для суммы конечного числа векторов.

Графическое изображение - свойства проекций

Нужна помощь в написании работы?

Мы - биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Примеры нахождения проекции

[stextbox id=”warning” caption=”Пример 1″]

Задача

Найти проекцию вектора $\overline{a} = (1, 2)$ на вектор $\overline{b} = (3, 4)$

Решение

Сначала находим скалярное произведение вектора:

$\overline{a}$ x $\overline{b}$ = $1$ x $3 + 2$ x $4$ = $3 + 8 = 11$ .

Найдём модуль вектора $\overline{b}$ :

$\overline{|b|}$ = $\sqrt{3^2 + 4^2}$ = $\sqrt{9 + 16}$ = $\sqrt{25} = 5$

Найдём проекцию вектора $\overline{a}$ на вектор $\overline{b}$

$pr_\overline{b}$ x $\overline{a}$ = $\overline{a}$ x $\overline{b}\over{|\overline{b}|}$ = $11\over{5}$ = $2,2$

Ответ: $pr_\overline{b}$ $\overline{a}$ = $2,2$

[/stextbox]

[stextbox id=”warning” caption=”Пример 2″]

Задача

Вычислить числовую проекцию вектора $\overline{a}$ на ось, направление которой определяется вектором $\overline{b}$ , если модуль вектора $\overline{a}$ равен 3, а угол между векторами $\overline{a}$ и $\overline{b}$ равен $30^0$ .

Решение

Итак, у нас есть $\overline{a}$ = $3$ $(\overline{a}$ , ^ $\overline{b}$ = $30^0$ , тогда искомая числовая проекция

$pr_\overline{b}$ . $\overline{a}$ = $3$ x $cos 30^0$ = $3$ x $\sqrt{3}\over{2}$ = $3\sqrt3\over{2}$ .

Ответ: $pr_\overline{b}$ . $\overline{a}$ = $3\sqrt3\over{2}$

[/stextbox]

[stextbox id=”warning” caption=”Пример 3″]

Задача

Вектор $\overline{b} = (-1, 0)$ задает направление оси $l$ . Найдите числовую проекцию вектора $\overline{a} = (-3, 4)$ на эту ось.

Решение

Скалярное произведение векторов, заданных своими координатами, равно сумме произведений соответствующих координат, то есть для данных векторов имеем:

$\overline{a}, \overline{b}$ = $-3$ x $(-1) +4$ x $0$ = $3 + 0$ = $3$

Модуль вектора $\overline{b}$ равен корню квадратному из суммы квадратов координат:

$|\overline{b}|$ = $\sqrt{-1^2 + 0^2}$ = $\sqrt{1 + 0}$ = $\sqrt{1}$ = $1$

Тогда: $pr_l\overline{a}$ = $pr_b$ . $\overline{a}$ = $3\over{1}$ = $3$

Ответ: $pr_l\overline{a}$ = $3$ .

[/stextbox]

Нашли ошибку? Выделите текст и нажмите CTRL + Enter

сагдиана на Решить уравнение с дробями онлайнничего не понятно!
акмарал на Более 50 основных формул по физике с пояснениема эти формулы обычно используют в олимпиядах
всем пока на Решить уравнение с дробями онлайнничего не понятно. калькулятор не работает.
Великий гей Никола Тесла на Более 50 основных формул по физике с пояснениемСайт параша, я пытался списать ЕГЭ по физике с помощью них, я блять сдал его на 99999 балов, и теперь
некто на Примеры решения матриц с ответамиНеправильные ответы, учите матрицу гении