Полярная система координат

Полярная система координат

Полярная система координат на плоскости вводится при помощи полярной оси (начало координат называется полюсом) и угла поворота этой оси (положительным считается направление против часовой стрелки) (рис. 1)

Рис. 1

Координаты точки в такой системе выглядят . Если не ограничивать значения и , тогда точки совпадают, то есть, между множеством точек плоскости и множеством пар числе нет взаимно однозначного соответствия. Для того, чтобы такое соответствие существовало, нужно рассмотреть так званые главные значения полярных координат, то есть, , . Дальше рассматриваются только такие значения.

Связь между полярными и прямоугольными (декартовыми) координатами легко понять из рис. 2, а именно,

(1)

и наоборот, полярные координаты выражаются через прямоугольные

 =

(2}

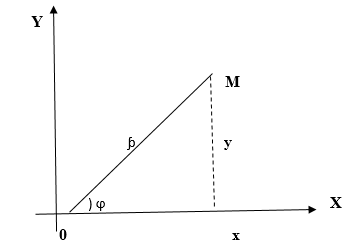
Рис. 2 

Чтобы найти во (2), учитываем совпадение знаков и , а также и .

Наведём графики некоторых линий в полярных координатах.

Луч

Пусть луч выходит с полюса под углом к полярной оси. Тогда уравнение луча (рис. 3).

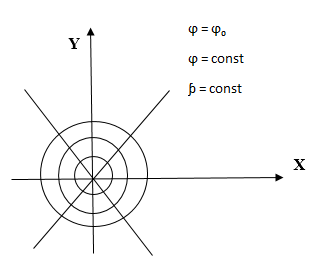
Рис. 3

Круг

Общее уравнение круга с центром в и радиусом имеет вид:

.

 Это уравнение может быть упрощено для отдельных случаев, например,

Или по-другому: радиуса ,  центр которого в полюсе имеет уравнение:

.

Спираль Архимеда

Имеет такой вид: , где – заданное действительное число.

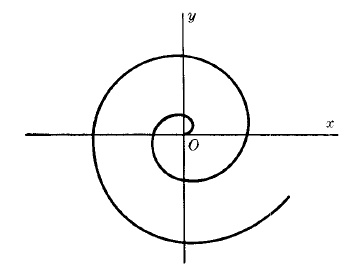
Рис. 4

Кардиоида

Кардиоида описывается уравнением , где заданное:

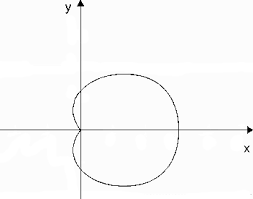
Рис. 5

Розы

Розами называются линии, которые задаются уравнением:

или ,

где и – дополнительные числа.

Так как , , тогда из уравнений получается, что , а это означает, что вся линия расположена в середине круга радиуса . Функция – периодическая и её график складывается из одинаковых лепестков, каждая из которых симметрична относительно наибольшего значения полярного радиуса . Количество лепестков зависит от числа :

при – целом и непарном роза складывается из лепестков (см. рис. 6);

при – целом и парном роза складывается из лепестков (см. рис. 7):

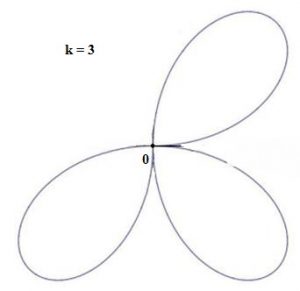
Рис. 6

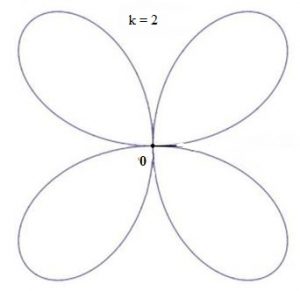
Рис. 7

Задача и её решение

[stextbox id=”warning” caption=”Пример”]

Задача

Построить в полярных координатах график функции , записав таблицу значений в градусах с шагом в . Перейти в уравнение к декартовым координатам.

Решение

Заполним таблицу значений аргумента и функции .

За данными таблицы строим точки в полярной системе координат и соединяем их плавной линией.

Перейдём в уравнение  от полярных координат к декартовым при помощи формулы перехода (1) и (2)

– это круг.

Чтобы найти центр и радиус круга, выделим главный квадрат:

.

Центр круга в точке , радиус (см. рис. 8)

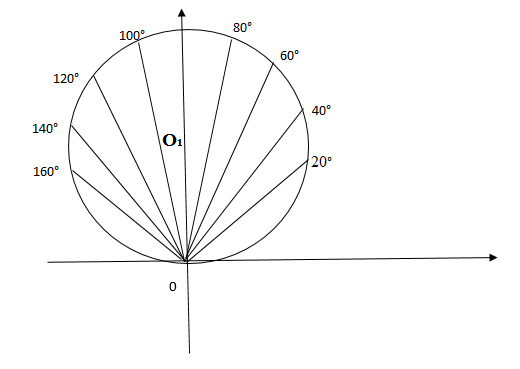
Рис. 8

Для построения графика провели лучи под соответствующими углами: . На каждом из лучей откладывается соответствующее значение , которое бралось из таблицы:

.

[/stextbox]