О чем статья

История теоремы

Однако название получено в честь учёного только по той причине, что он первый и, даже единственный человек, который смог доказать теорему.

Немецкий историк математики Кантор утверждал, что о теореме было известно ещё египтянами приблизительно в 2300 году до н. э. Он считал, раньше строили прямые углы благодаря прямоугольным треугольникам со сторонами 3, 4 и 5.

Известный учёный Кеплер говорил, что у геометрии есть незаменимое сокровище — это теорема Пифагора, благодаря которой можно вывести большинство теорем в геометрии.

Раньше теорему Пифагора называли “теоремой невесты” или “теоремой нимфы”. А всё дело в том, что её чертёж был очень похож на бабочку или нимфу. Арабы же, когда переводили текст теоремы, решили, что нимфа означает невеста. Так и появилось интересное название у теоремы.

Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.

Подробнее

Теорема Пифагора, формула

[stextbox id=»teorema» defcaption=»true»]

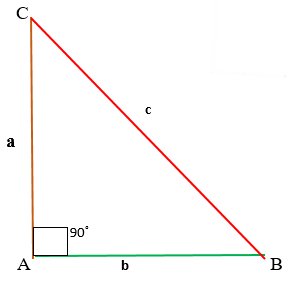
Теорема Пифагора — в прямоугольном треугольнике сумма квадратов катетов ( $a,b$ ) равна квадрату гипотенузы ( $c$ ). Это одна из основополагающих теорем эвклидовой геометрии.

Формула: $a^2 + b^2 = c^2$

[/stextbox]

Как уже говорилось, есть много разнообразных доказательств теоремы с разносторонними математическими подходами. Однако, более часто используют теоремы, связанные с площадями.

Построим на треугольнике квадраты (синий, зеленый, красный)

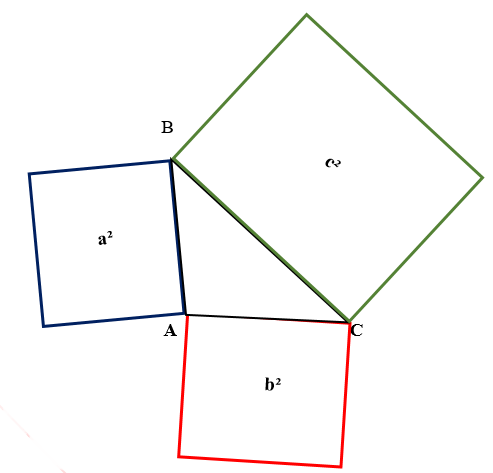
То есть сумма площадей квадратов, построенных на катетах равняется площади квадрата, построенном на гипотенузе. Соответственно, площади этих квадратов равны — $a^2, b^2, c^2$ . Это и есть геометрическое объяснение Пифагора.

Доказательство теоремы методом площадей: 1 способ

Докажем, что $c^2 = a^2 + b^2$ .

Рассмотрим всё тот же треугольник с катетами a, b и гипотенузой c.

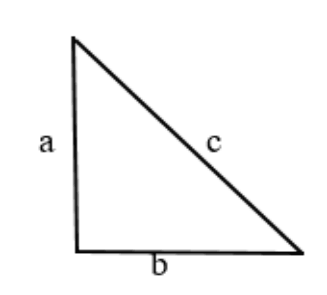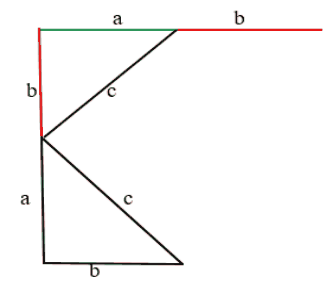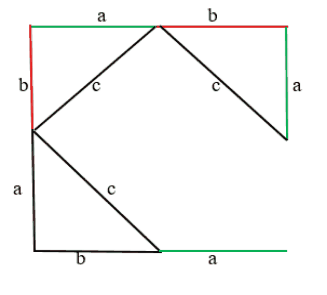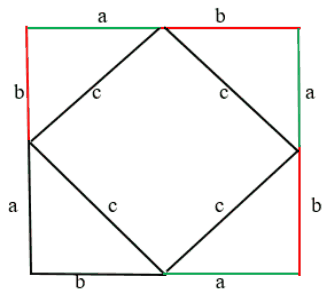
Достраиваем прямоугольный треугольник до квадрата. От катета “а” продолжаем линию вверх на расстояние катета “b” (красная линия).
Далее ведём линию нового катета “а” вправо (зелёная линия).
Два катета соединяем гипотенузой “с”.

Получается такой же треугольник, только перевёрнутый.

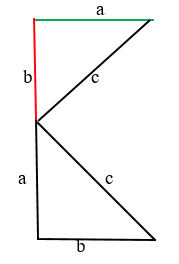
Аналогично строим и с другой стороны: от катета “а” проводим линию катета “b” и вниз “а” и “b” А снизу от катета “b” проводим линию катета “а”. В центре от каждого катета провели гипотенузы “с”. Таким образом гипотенузы образовали квадрат в центре.

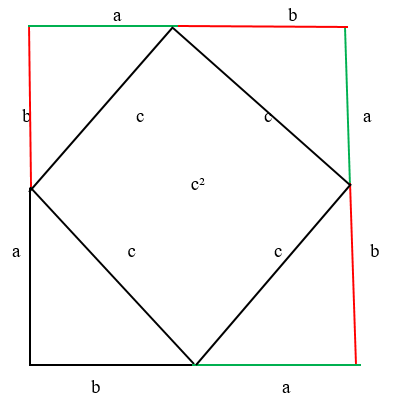
Этот квадрат состоит из 4-х одинаковых треугольников. А площадь каждого прямоугольного треугольника = половина произведения его катетов. Соответственно, ${1\over{2}}ab$ . А площадь квадрата в центре = $c^2$ , так как все 4 гипотенузы со стороной $c$ . Стороны четырёхугольника равны, а углы прямые. Как нам доказать, что углы прямые? Очень просто. Возьмём всё тот же квадрат:

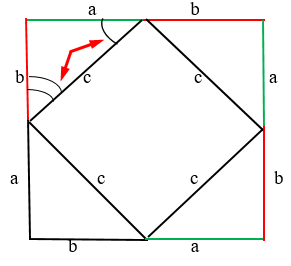
Мы знаем, что эти два угла, показаны на рисунке, являются 90 градусам. Так как треугольники равны, значит следующий угол катета “b” равен предыдущему катету “b”:

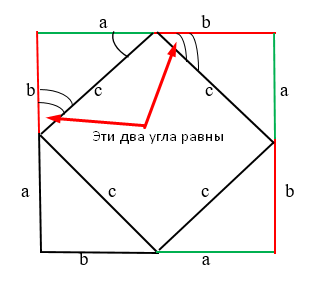
Сумма этих двух углов = 90 градусов. Соответственно, предыдущий угол тоже 90 градусов. Конечно же, аналогично и с другой стороны. Соответственно, у нас действительно квадрат с прямыми углами.

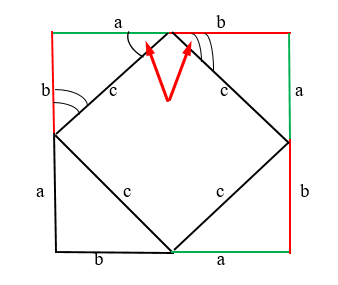
Так как острые углы прямоугольного треугольника в общей сложности равняются 90 градусам, то угол четырёхугольника так же будет равен 90 градусов, ведь 3 угла в сумме = 180 градусов.

Соответственно, площадь квадрата складывается из четырёх площадей одинаковых прямоугольных треугольников и площади квадрата, который образован гипотенузами.

Таким образом, получили квадрат со стороной $a + b$ . Мы знаем, что площадь квадрата со стороной $a + b$ — это будет квадрат его стороны. То есть $(a + b)^2$ . Этот квадрат состоит из четырёх одинаковых треугольников.

Запишем: $(a + b)^2 = 4$ .
Далее смотрим, что площадь прямоугольного треугольника — это половина произведения его катетов. Поэтому дальше записываем:т $(a + b)^2 = 4 * {1\over{2}}$
Также надо прибавить площадь квадрата, который находится в центре между треугольниками со стороной “с”. И теперь получим: $(a + b)^2 = 4 * {1\over{2}} + c^2$

Раскрываем скобки и получаем: $a^2 + b^2 + 2ab = 2ab + c^2$
Сокращаем $2ab$ . Получается: $a^2 + b^2 = c^2$

И это значит, что мы доказали теорему Пифагора.

ВАЖНО!!! Если находим гипотенузу, тогда складываем два катета, а затем ответ выводим из корня. При нахождении одного из катетов: из квадрата длины второго катета вычитаем квадрат длины гипотенузы и находим квадратный корень.

Примеры решения задач

[stextbox id=»warning» caption=»Пример 1″]

Задача

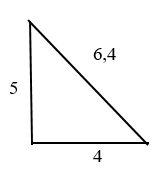
Дано: прямоугольный треугольник с катетами 4 и 5.

Найдите гипотенузу. Пока её обозначим “с”

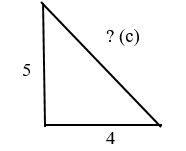
Решение

Сумма квадратов катетов $5^2 + 4^2$ равняется квадрату гипотенузы. В нашем случае — $c^2$ .

Воспользуемся теоремой Пифагора: $5^2 + 4^2 = c^2$

Итак, $5^2 = 25$ , а $4^2 = 16$ . Катеты в сумме получают 41.

Тогда $41 = c^2$ . То есть квадрат гипотенузы равен 41.

Квадрат числа 41 = 6,4.

Мы нашли гипотенузу.

Ответ

Гипотенуза = 6,4

[/stextbox]

[stextbox id=»warning» caption=»Пример 2″]

Задача

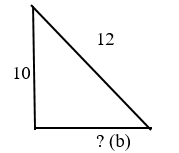
Дано: прямоугольный треугольник, где гипотенуза = 12, один катет = 10

Найдите второй катет.

Решение

Обозначим неизвестный катет — b.

Воспользуемся теоремой Пифагора:

$10^2 + b^2 = 12^2$

$10^2 = 100$ , а $12^2 = 144$

Запишем:

$100 + b^2 = 144$

Находим $b^2$

$b^2 = 144 - 100$

$b^2 = 44$

Если $b^2 = 44$ , тогда просто $b = 6,6$

Ответ

Второй катет (b) равен 6,6.

[/stextbox]

Заключение

Доказательство теоремы Пифагора (анимация)

Итак, мы рассмотрели теорему Пифагора, смогли привести ее доказательство и привели несколько примеров задач и их решений.

Запомните раз и навсегда: квадраты гипотенузы равен суммы квадратов катетов: $a^2 + b^2 = c^2$ (это вся теорема Пифагора).

Нашли ошибку? Выделите текст и нажмите CTRL + Enter

сагдиана на Решить уравнение с дробями онлайнничего не понятно!
акмарал на Более 50 основных формул по физике с пояснениема эти формулы обычно используют в олимпиядах
всем пока на Решить уравнение с дробями онлайнничего не понятно. калькулятор не работает.
Великий гей Никола Тесла на Более 50 основных формул по физике с пояснениемСайт параша, я пытался списать ЕГЭ по физике с помощью них, я блять сдал его на 99999 балов, и теперь
некто на Примеры решения матриц с ответамиНеправильные ответы, учите матрицу гении

Теорема Пифагора

История теоремы

Теорема Пифагора, формула

Доказательство теоремы методом площадей: 1 способ

Примеры решения задач

Заключение

Авторизуйтесь