vektory — ресурсы и инструменты для работы с векторной графикой

Скалярные и векторные величины

Векторные величины — величины, для характеристики которых указывается как числовое значение, так и направление в пространстве. Например, сила, скорость, ускорение, напряженность поля (магнитного, электромагнитного) и т. п.

Скалярные величины — это величины, для характеристики которых достаточно только числовое значение в соответствующих единицах измерения. Например, масса, температура, длина, площадь, объём, количества тепла и т. д.

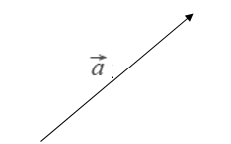
Рис. 1

Вектор — это геометрическое изображение векторной величины в заданном масштабе.

На рис. 1 А — начальная точка вектора, В — конец вектора. Вектор обычно обозначается стрелочками, которые ставят вверху букв, но многие люди для удобства ставят обычные чёрточки.  Иногда вектор обозначают одной буквой: . Расстояние от точки к точке называют длиной или модулем вектора, а обозначается так:  или

Если начало и конец вектора совпадают, тогда такой вектор называется нулевым и обозначается Направление нулевого вектора может быть произвольным.

 [stextbox id=»info» defcaption=»true»]Два ненулевых вектора, которые лежат на параллельных прямых или на одной прямой называются коллинеарными, а обозначаются [/stextbox]

Нулевой вектор считается коллинеарным производного вектора.

 [stextbox id=»info» defcaption=»true»]Векторы, которые параллельны одной и той же плоскости, или те, которые лежат в одной плоскости, называются компланарными.[/stextbox]

 [stextbox id=»info» defcaption=»true»]

Равными называются векторы, если они удовлетворяют такие условия:

1) они коллинеарны;

2) их модули равны;

3) они направлены в одну сторону, то есть:

= = ,

[/stextbox]

 Например, на рис. 2, где ABCD — параллелограмм,

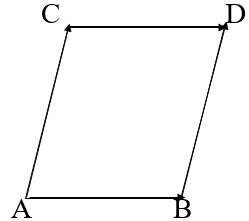
Рис. 2

где векторы = , = .

Если = , , тогда векторы и — противоположные.

Вектор противоположный вектору обозначают . Вектор  противоположен вектору  и записывается  = 

 [stextbox id=»info» defcaption=»true»]

Из определения равенства векторов следует, что вектор можно переносить в пространстве параллельно самому себе, такие векторы называются свободными.

[/stextbox]

Вектор, модуль которого равен единице называется единичным, или ортом, и обозначается :

= ,

Линейные операции над векторами: сложение векторов, вычитание и умножение

Линейные операции над векторами или ещё говорят действия над векторами — это сложение векторов, вычитание и умножение вектора на число (скаляр).

Сложение векторов

Пусть заданы два вектора и . Отложим с некоторой точки вектор = , а тогда из точки отложим вектор = и рассмотрим вектор = .

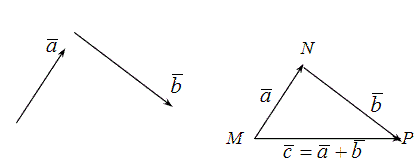
Рис. 3

[stextbox id=»info» defcaption=»true»]Сумма двух векторов и называется вектор = , начало которого  находится в начале вектора , а окончание в конце вектора при условии, что начало находится в конце .[/stextbox]

Согласно рис. 3 вектор = и замыкает ломаную MNP, направление вектора берётся в конец последнего слагаемого .

По принципу замыкания находится сумма большего числа слагаемых.

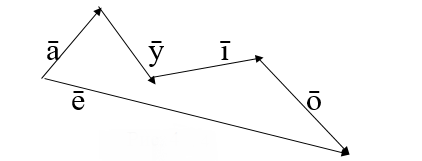
Рис. 4

Вычитание векторов

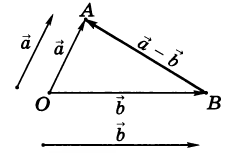
Рис. 5

Посмотрите на рис. 5. Мы поместили начало векторов и в одну точку , и построили замыкающий вектор .

[stextbox id=»info» defcaption=»true»]Разница двух векторов — это , которые выходят  с одной точки, называются замыкающим вектором (обозначается ), направление которого выбирается в сторону уменьшаемого.[/stextbox]

Умножение вектора на число

[stextbox id=»info» defcaption=»true»]Произведением ненулевого вектора  на число называется вектор и обозначается (), коллинеарный  вектору , модуль которого .[/stextbox]

Направление вектора совпадает с направлением вектора , если , и противоположному направлению вектора , если .

При , или считается, что  — нулевой вектор.

Рис. 6

Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.

Подробнее

Свойства векторов

Мы рассмотрели линейные операции над векторами и теперь можно рассмотреть свойства векторов, без которых невозможно решить многие задачи.

1).

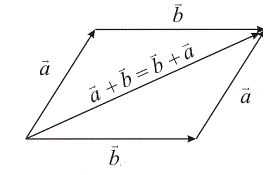
Рис. 7

Свойство 1 называется переставным или коммутативным, понятно с рис. 7, что разрешается прибавлять векторы по правилу параллелограмма.

2). — ассоциативное  или соединительное свойство (см. рис. 8).

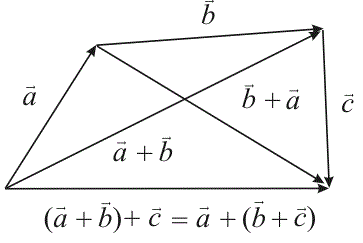
Рис. 8

3). .

4). .

5). x .

6). = .

7). x .

8). .

Свойства 3 — 8 вы уже сможете проверить самостоятельно.

Примеры

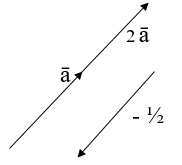
[stextbox id=»warning» caption=»Пример 1″]

За данными вектора и построить векторы:

а) ,

б) .

Решение покажем на рисунке:

Первый рисунок решения a:

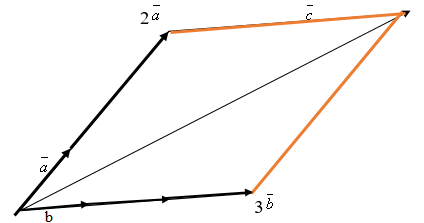
Второй рисунок решения б:

[/stextbox]

[stextbox id=»warning» caption=»Пример 2″]

В треугольнике проведена медиана (см. на рис. ниже). Выразить вектор через векторы и .

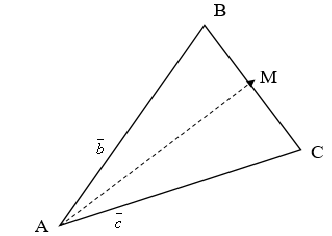
Решение:

Согласно определению о разнице векторов — , тогда   = = — .

Согласно определению суммы векторов с у нас получается:

x = x .

[/stextbox]