О чем статья
Парабола
Чтобы получить каноническое уравнение параболы, расположим директрису перпендикулярно оси $OX$, а фокус $F$ на оси $OX$ так, чтобы начало координат $O(0, 0)$ помещался на одинаковом расстоянии от них (см. рис. 1). Обозначим через $p$ расстояние от фокуса к директрисе, тогда у фокуса будут координаты ${x} = {p\over{2}}$, $y = 0, F({p\over{2}}, 0)$.
Для произвольной точки $M (x, y)$ параболы расстояний $FM = r$, а расстояние к директрисе $MN = d$. По определению $d = r$ из рис. 1 видим, что $d = {x} + {p\over{2}}$, а ${r} = \sqrt{x – {p\over{2}}^2} + y^2$ и поэтому:
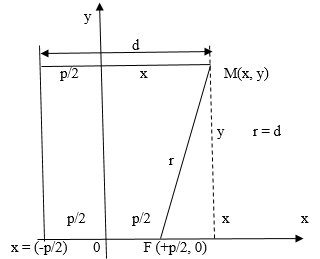
Рис. 1
$\sqrt{(x – {p\over{2}})^2 + y^2} = x + {p\over{2}}\to{x}^2 – 2 * {p\over2}}x + {p^2\over{4}} + y^2 = x^2 + 2 * {p\over{2}}x + {p^2\over{4}}$
$y^2 = 2px$
(1)
– каноническое уравнение параболы.
Нужна помощь в написании работы?
Мы - биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Что такое вершина параболы
Вершина параболы – это парабола, которая проходит через точки $O (0, 0)$. Если точка $M_{1}(x , y)$ принадлежит параболе, то и $M_{2}(x , -y)$ тоже принадлежит параболе, так как из:
$y^2 = 2px\to{(-y)^2 = 2px}$.
Значит, парабола симметрична относительно оси $OX$, её график достаточно построить в первой четверти, где из канонического уравнения параболы получается, что:
$y = \sqrt{2px}$
Чтобы найти вершину параболы, необходимо знать формулу: $ax^2 + bx + c = 0$.
Давайте посмотрим, как данная формула действует, допустим дано уравнение:
$y^2 = x^2 + 9x + 18$
Тогда:
$a = 1$, $b = 9$, $c = 18$. Чтобы найти величины $a$, $b$ и $c$, в квадратном уравнении коэффициент при $x^2 = a$, при $x = b$, постоянная (коэффициент без переменной) = $c$. Если взять тот же пример, $y^2 = x^2 + 9x + 18$, получается, что:
$x = {-b\over{2a}}$, $x = {-9\over{2 * 1}}$, $x = {-9\over{2}}$.
Форма и характеристики параболы
Исследуем за каноническим уравнением форму и расположение параболы:
1. В уравнении $y^2 = 2px$ переменная входит в парной степени откуда получается, что парабола симметрична относительно оси $OX$. Ось $OX$ – это ось, которая симметрична параболе.
2. Так как $p > 0$, тогда $x\geq{0}$, откуда получается, что парабола расположена справа от оси $Oy$.
3. При $x = 0$ мы имеем $y = 0$, то есть парабола проходит через начало координат. Точка $O(0, 0)$ – это вершина параболы.
4. При увеличении значений переменной $x$ модуль $y$ тоже возрастает. Изобразим параболу на рисунке:
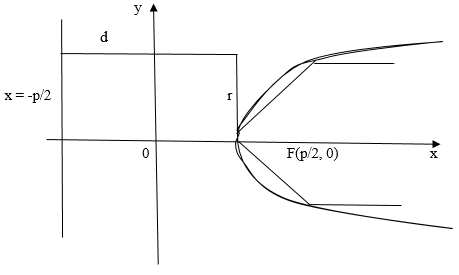
Рис. 2
5. В полярной системе координат, у канонического уравнения параболы такой вид:
${r} = {p\over{1 – cos\varphi}}$
6. Уравнение $y^2 = – 2px$, $x^2 = 2py$, $x^2 = -2py (p > 0)$, тоже описывают параболы:
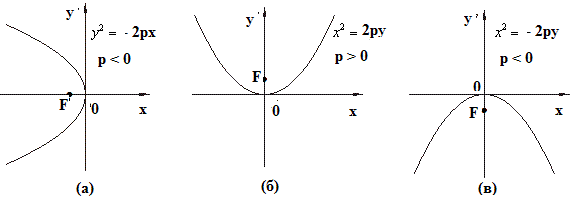
Рис. 3
Оптическое свойство параболы
У параболы “оптическое” свойство, если: в фокусе параболы поместить источник света, тогда отбитые от параболы лучи будут параллельными оси $OX$. Это свойство учитывают при изготовлении прожекторов, зеркальных телескопов, теле- и радио антенн.
При положительном $p$ уравнении:
$y = – 2px$
описывают параболу симметричную относительно $OX$ с вершиной в точке $O(0, 0)$, ветви которой направлены влево (рис. 3 (а)).
Аналогично изложенному, уравнение $x^2 = 2py$ и $x^2 = -2py$ описывают параболы с вершиной в точке $O(0, 0)$ симметрично относительно $OY$, ветви которой направлены соответственно вверх и вниз (см. рис. 3 (б) и (в)). Если например, уравнение $x^2 = 2py$ решить относительно $y$
$y = {1\over{2p}}x^2$ и обозначить ${1\over{2p}} = a$, тогда получим известное со школьного курса уравнение параболы $y = ax^2$. Теперь её фокусное расстояние ${p\over{2}} = {1\over{4a}}$.
Примеры решения
Задача
Найти координаты фокуса и составить уравнение директрисы параболы $y^2 = 6x$.
Решение
Сравнивая каноническое уравнение $y^2 = 2px$ и данное $y^2 = 6x$, получим $2p = 6\to{p = 3$, ${p\over{2}} = {3\over{2}}$, тогда$F ({3\over{2}}, 0)$. Так как уравнение директрисы $x = -{p\over{2}}$, тогда в данном случае $x = -{3\over{2}}$.
Ответ
координаты фокуса: $F ({3\over{2}}, 0)$, а уравнение директрисы параболы: $x = -{3\over{2}}$.
Задача
Составить каноническое уравнение параболы:
а) с фокусом в точке $F(2, 0)$;
б) с фокусом в точке $F(0, -6)$.
Решение
а). Так как фокус $F(2, 0)$ на положительной полуоси $OX$, тогда парабола симметрична относительно $OX$ с вершиной в точке $O(0, 0)$ и ${p\over{2}} = 2$, поэтому $p = 4$ и согласно формуле (1) $y^2 = 8x$.
б). Фокус $F(0, -6)$ лежит на отрицательной полуоси $OY$ с вершиной в точке $O(0, 0)$, ветви направлены вниз, каноническое уравнение следует искать в виде $x^2 = -2py$. Фокусное расстояние параболы $|OF| = {p\over{2}} = 6\to{p} = 12$ и уравнение запишется $x^2 = -24y$.
Ответ
а) каноническое уравнение параболы с фокусом в точке $F(2, 0)$: $y^2 = 8x$;
б) каноническое уравнение с фокусом в точке $F(0, -6)$: $x^2 = -24y$.
Задача
Показать путём выделения полного квадрата, что уравнение $4x^2 – 12x + y + 6 = 0$ – это уравнение параболы. Привести его к каноническому виду. Найти вершину, фокус, ось и директрису этой параболы.
Решение
Выделим относительно переменной $x$ полный квадрат
$(4x^2 – 12x) + y + 6$ = $0\to{4(x^2 – 3x)} + y + 6$ = $0\to{4((x^2 – 2 * {3\over{2}}x + {9\over{4}}) – {9\over{4}}) + y + 6$ = $0}\to{4((x – {3\over{2}}})^2 – 9 + y + 6$ = $0\to{y – 3$ = $-4(x – {3\over{2}})^2}\to{(x – {3\over{2}})^2}$ = $-{1\over{4}}(y – 3)$.
Обозначим $y_{1} = y – 3$, $x_{1} = x – {3\over{2}}$. Тогда в результате параллельного переноса координатных осей в новое начало, то есть в точку $O_{1}({3\over{2}}, 3)$, получим каноническое уравнение параболы ${x_{1}^2} = -{1\over{4}}y_{1}$.
Ветви этой параболы направлены вниз симметрично относительно оси $O_{1}Y_{1}$, $2p = {1\over{4}}\to{p} = {1\over{8}}$, ${p\over{2}} = -{1\over{16}}$ – фокусное расстояние. В новой системе координат фокус находится в точке $F(0, -{1\over{16}})$, уравнение директрисы в новой системе $y_{1} = {1\over{16}}$.
Повернёмся к старым координатам при помощи замены $y_{1} = y – 3$, $x_{1} = x – {3\over{2}}$. Уравнение оси в новой системе $x_{1} = 0$, а в старой $x – {3\over{2}} = 0\to {2x – 3 = 0}$ – уравнение оси параболы.
Уравнение директрисы в новой системе координат $y_{1} = {1\over{16}}$, а в старой $y – 3 = {1\over{16}}\to{y – {49\over{16}}} = 0\to{16y – 49} = 0$.
В новой системе $X_{1}O_{1}Y_{1}$ для фокуса $F(0, -{1\over{16}}) x_{1} = 0$, $y_{1} = -{1\over{16}}$, а в старой системе $x_{F} – {3\over{2}} = 0\to{x_{F}} = {3\over{2}}$, $y_{F} – 3 = -{1\over{16}}\to{y_{F} = -{1\over{16}} + 3\to{y_{F}} = {47\over{16}}$, то есть $F({3\over{2}}, {47\over{16}})$.
Ответ
Каноническое уравнение параболы – ${x_{1}^2} = -{1\over{4}}y_{1}$;
вершина – ветви параболы направлены вниз;
$O_{1}Y_{1}$, $2p = {1\over{4}}\to{p} = {1\over{8}}$, $p_{2} = -{1\over{16}}$ – фокусное расстояние, а фокус находится в точке $F(0, -{1\over{16}})$;
уравнение оси $x_{1} = 0$;
уравнение директрисы $y_{1} = {1\over{16}}$.