Базис векторов и линейные действия над векторами аналитическим путём (теория и решение задач)

О чем статья

Базис векторов

[stextbox id=”info” defcaption=”true”]Система линейно независимых векторов пространства, за которыми можно разложить произвольный вектор – это и есть базис векторов или этого пространства.[/stextbox]

Так, согласно доказательству (3), произвольные три некомпланарные векторы $\overrightarrow{l_1}$ , $\overrightarrow{l_2}$ , $\overrightarrow{l_3}$ , образуют в трёхмерном пространстве базис, по которому, согласно формуле (2) можно единственным образом разложить произвольный вектор $\overrightarrow{a}$ пространства. Векторы $\overrightarrow{l_1}$ , $\overrightarrow{l_2}$ , $\overrightarrow{l_3}$ , которые образуют базис называются базисными.

Будем считать, что базисные векторы $\overrightarrow{l_1}$ , $\overrightarrow{l_2}$ , $\overrightarrow{l_3}$ сведены к точке $O$ .

Числ $\alpha, \beta, \gamma$ , про которые упоминалось в разделах “линейно зависимая и линейно независимые системы векторов”, называют координатами вектора в заданном базисе, и пишут:

$\overrightarrow{a} = \alpha\overrightarrow{l_1} + \beta\overrightarrow{l_2} + \gamma\overrightarrow{l_3} = (\alpha, \beta, \gamma)$ .

Аналогично, на плоскости базис образуют какие-то два неколлинеарные векторы, а любой некомпланарный с ними может быть разложен по этому базису.

Базисным вектором на прямой линии может быть любой ненулевой вектор.\Согласно свойствам линейных операций над векторами, следует, что при сложении и вычитании векторов в данном базисе прибавляются и отнимаются их соответствующие координаты, а при умножении вектора на число умножаются не это число координаты вектора, то есть:

$\overrightarrow{a}\pm\overrightarrow{b} = (\alpha\overrightarrow{l_1} + \beta_{1}\overrightarrow{l_2} + \gamma_{1}\overrightarrow{l_3}) \pm ({\alpha_{2}\overrightarrow{l_1} + \beta_{2}\overrightarrow{l_2} + \gamma_{2}\overrightarrow{l_3}) = (\alpha_{1} \pm \alpha_{2}, \beta_{1} \pm \beta_{2}, \gamma_{1} \pm \gamma_{2})$ .
$\lambda\overrightarrow{a} = \lambda(\alpha\overrightarrow{l_1} + \beta\overrightarrow{l_2} + \gamma\overrightarrow{l_3}) = (\lambda\alpha, \lambda\beta, \lambda\gamma)$ .
$\overrightarrow{a} = \overrightarrow{b} \Longleftrightarrow \alpha_{1} = \alpha_{2}, \beta_{1} = \beta_{2}, \gamma_{1} = \gamma$ .

[stextbox id=”danger” defcaption=”true”]Векторы равны, когда у них одинаковые соответствующие координаты.[/stextbox]

Линейные действия над векторами аналитическим путём

Если раньше линейные действия над векторами осуществлялись графически, то теперь эти операции можно выполнять аналитически, не пользуясь рисунком. Давайте вспомним и сформулируем линейные действия:

Чтобы прибавлять (отнимать) два вектора, необходимо прибавить (отнять) их соответствующие координаты, то есть: $\overrightarrow{a} \pm \overrightarrow{b} = (x_{1}\overrightarrow{b} + y_{1}\overrightarrow{c}) \pm (x_{2}\overrightarrow{b} + y_{2}\overrightarrow{c} + z_{2}\overrightarrow{o}) = (x_{1} \pm x_{2})\overrightarrow{a} + (y_{1} \pm y_{2})\overrightarrow{c} + (z_{1} \pm z_{2})\overrightarrow{o} = (x_{1} \pm x_{2}), y_{1} \pm y_{2}, z_{1} \pm x_{2}).$

Приведём пример:

[stextbox id=”warning” caption=”Пример 1″]

Найти сумму векторов $\overrightarrow{a} = 4 \overrightarrow{i} - 2 \overrightarrow{j} = (4, -2)$ и $\overrightarrow{b} = 2 \overrightarrow{i} + 5\overrightarrow{j} = (2, 5)$ , заданных на плоскости $XOY$ .

Решение:

Согласно правилу 1 у нас получается:

$\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b} = (4\overrightarrow{i} - 2\overrightarrow{i}) + (2\overrightarrow{i} + 5\overrightarrow{j}) = (4 + 2)\overrightarrow{i} + (-2 + 5)\overrightarrow{j})$ = (6, 3).

Построим эти векторы: $\overrightarrow{a} = \overrightarrow{OA}, \overrightarrow{b} = \overrightarrow{OB}, \overrightarrow{c} = \overrightarrow{OC}$ .

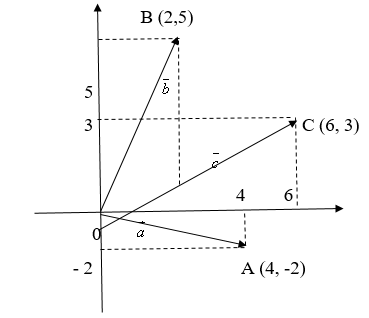
Рис. 3 - декартова система координат

Рис. 3

Мы видим, что четырёхугольник OABC – параллелограмм. Координаты вектора $\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b} = (6, 3)$ мы сначала получили путём вычислений (аналитически), без помощи рисунка. Рисунок только подтверждает правило параллелограмма при прибавлении векторов, поэтому дальше рисунками будем пользоваться для наглядности.

[/stextbox]

Чтобы умножить вектор на число, необходимо каждую из его координат умножить на это число:

$\lambda\alpha = \lambda(x \overrightarrow{b} + y\overrightarrow{c} + z \overrightarrow{o}) = \lambda\x \overrightarrow{b} + \lambda\y\overrightarrow{c} + \lambda\z \overrightarrow{o} = (\lambda x, \lambda y, \lambda z),$

[stextbox id=”warning” caption=”Пример 2″]

Дан вектор $\overrightarrow{a} = (1, -1, 2).$ Найти $\overrightarrow{b} = - 2 \overrightarrow{a}$

Решение:

Согласна правилу 2 у нас получается:

$\overrightarrow{b} = -2( \overrightarrow{i} - 2 \overrightarrow{j} + 2 \overrightarrow{k}) = -2 \overrightarrow{i} + 4 \overrightarrow{j} - 4 \overrightarrow{k} = (-2, 4, -4),$

Геометрическое изображение смотрите на рис. 4.

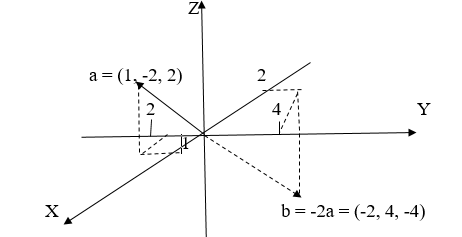
Рис. 4 - декартова система координат

Рис. 4

[/stextbox]

Два вектора равны, если у них равны соответствующие координаты:

$\overrightarrow{a} = \overrightarrow{b} \longleftrightarrow (x_{1} = x_{2}, y_{1} = y_{2}, z_{1} = z_{2})$ .

Теперь вы понимаете, как получить координаты вектора не только графическим путём, но и аналитическим. В дальнейшем у вас не возникнет сложностей по этому поводу.

Как найти базис вектора, пример

[stextbox id=”warning” caption=”Пример 1″]

В некотором базисе заданы своими координатами векторы $\overrightarrow{a} = (2, 1), \overrightarrow{b} = (3, 4)$ и $\overrightarrow{m} = (-1, 2).$ Разложить вектор $\overrightarrow{m}$ по базису, который образовался из векторов $\overrightarrow{a}$ и $\overrightarrow{b}.$

Решение:

Разложение вектора $\overrightarrow{m}$ по базису $\overrightarrow{a}$ и $\overrightarrow{b}$ имеет такой вид:

$\overrightarrow{m} = \alpha\overrightarrow{a} + \beta\overrightarrow{b},$

где числа $\alpha$ и $\beta$ – неизвестные. Чтобы их найти, подставим в последнее равенство координаты векторов $\overrightarrow{m}, \overrightarrow{a},$ и $\overrightarrow{b}$ , а тогда воспользуемся свойствами 1 и 2:

$\alpha (2, 1) + \beta (3, 4) = (-1, 2)\\ (2\alpha, \alpha) + (3\beta, 4\beta) = (-1, 2)\\ (2 \alpha + 3 \beta, \alpha + 4 \beta) = (-1, 2)$

Согласно свойству 3 про равенство векторов, получим систему уравнений:

$\left\{ \begin{aligned} 2 \alpha + 3 \beta = -1\\ \alpha + 4 \beta = 2 \end{aligned} \right|$

Первое равенство умножаем на 1, а второе на (- 2) и в итоге у на получается:

$- 5 \beta = -5, \beta = 1, \alpha' = - 2$ .

Значит, ответ у нас выходит: $m = - 2 + b$

[/stextbox]

Нашли ошибку? Выделите текст и нажмите CTRL + Enter

сагдиана на Решить уравнение с дробями онлайнничего не понятно!
акмарал на Более 50 основных формул по физике с пояснениема эти формулы обычно используют в олимпиядах
всем пока на Решить уравнение с дробями онлайнничего не понятно. калькулятор не работает.
Великий гей Никола Тесла на Более 50 основных формул по физике с пояснениемСайт параша, я пытался списать ЕГЭ по физике с помощью них, я блять сдал его на 99999 балов, и теперь
некто на Примеры решения матриц с ответамиНеправильные ответы, учите матрицу гении

Базис векторов и линейные действия над векторами аналитическим путём (теория и решение задач)