О чем статья

Параметрическое и каноническое уравнение прямой в пространстве

Параметрическое и каноническое уравнение прямой рассматривается практически так, как и для прямой на плоскости. Значит, нужно составить уравнение прямой $L$ , которая проходит через данную точку $M_{1} (x_{1}, y_{1}, z_{1})$ параллельно направляющему вектору $\overline{S} = (l, m, p)$ .

[stextbox id=”info” defcaption=”true”]

Пусть, $M(x, y, z) \in{L}$ – произвольная точка прямой, тогда векторы $\overline{M_{1}M} = (x - x_{1}, y - y_{1}, z - z_{1})$ и $\overline{S}$ коллинеарные, а это значит, что координаты их пропорциональны, поэтому получаем:

${x - x_{1}\over{l}} = {y - y_{1}\over{m}} = {z - z_{1}\over{p}}$

(1)

это и есть канонические уравнения прямой.

[/stextbox]

Приравнивая каждую из дробей (1) к параметру $t$ , запишем параметрические уравнения прямой:

$\left\{ \begin{aligned} x = lt + x_{0}\\ y = mt + y_{0}\\ z = pt + z_{0} \end{aligned}$

(2)

Уравнение прямой в пространстве, которая проходит через две заданные точки

Уравнение прямой в пространстве – тема очень лёгкая, так как здесь самое важное – знать нужную формулу. Тогда легко можно решить любую задачу.

Итак, через две точки $M_{1}(x_{1}, y_{1}z_{1}$ и $M_{2}(x_{2}, y_{2}, z_{2})$ можно не только геометрично провести линию, но и сложить её уравнения.

[stextbox id=”info” defcaption=”true”]

За направляющий вектор возьмём $\overline{S} = \overline{M_{1}M} = (x_{2} - x_{1}, y_{2} - y_{1}, z_{2} - z_{1})$ , тогда по формуле (1) у нас получается:

${x - x_{1}\over{x_{2} - x_{1}}} = {y - y_{1}\over{y_{2} - y_{1}}} = {z - z_{1}\over{z_{2} - z_{1}}}$

(3)

уравнение прямой в пространстве, которые проходят через две заданные точки.

[/stextbox]

Нужна помощь в написании работы?

Мы - биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Общее уравнение прямой – переход к каноническому уравнению

Объяснение про общее уравнение прямой начнём с прямой, которая задана двумя плоскостями, что пересекаются по этой прямой.

[stextbox id=”info” defcaption=”true”]

Пусть известны их уравнения:

$\left\{\begin{aligned}A_{1}x + B_{1}y + C_{1}z + D_{1} = 0\\A_{2}x + B_{2}y + C{2}z + D_{2} = 0 \end{aligned}$

(4)

Тогда система (4) называется общим уравнением прямой.

[/stextbox]

Чтобы перейти к каноническим уравнениям вида (1), необходимо найти вектор $\overline{S}$ и точку $M_{0}$ этой прямой.

Точку $M_{0}$ находим, как один из решений системы (4). Например, положив в (4) $z = 0$ находим $x_{0}, y_{0}$ , тогда и точку $M_{0} (x_{0}, y_{0}, 0)$ . Направляющий вектор $\overline{S}$ , который параллелен к каждой из плоскостей $P_{1}$ и $P_{2}$ и перпендикулярен к их нормальным векторам $\overline{n_{1}} = (A_{1}, B_{1}, C_{1})$ и $\overline{n_{2}} = (A_{2}, B_{2}, C_{2})$ , то есть $\overline{S}\perp{\overline{n_{1}}}$ , $\overline{S}\perp{\overline{n_{2}}}$ . (см. рис. 1). Поэтому вектор $\overline{S}$ можно найти при помощи векторного произведения $\overline{n_{1}}$ и $\overline{n_{2}}$

$\overline{S}$ = $\overline{n}_{1}$ x $\overline{n}_{2}$ = $\begin{vmatrix} \overline{i}&\overline{j}&\overline{k}\\ A_{1}&B_{1}&C_{1}\\ A_{2}&B_{2}&C_{2} \end{vmatrix}$

Найдены координаты $M_{0}$ и $\overline{S}$ подставим в каноническое уравнение (1).

Например, от общих уравнений прямой:

$\left\{\begin{aligned} 2x + 7y - z - 4 = 0\\ 4x - 9y - 2z - 8 = 0 \end{aligned}$

Перейдём к каноническим, положив в системе $y = 0$ (при нём относительно больше коэффициенты). найдём $x = 2, z = 0, M_{0} (2, 0, 0)$ . Нормальные векторы $\overline{n_{1}} = (2, 7, -1)$ и $\overline{n_{2}} = (4, -9, -2)$ . Тогда направляющий вектор

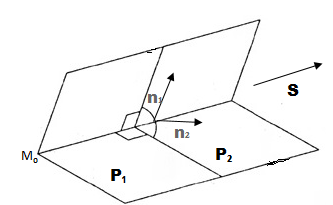
Уравнение прямой

Рис. 1

$\overline{S} = \overline{n}_{1}$ x $\overline{n}_{2}$ = $\begin{vmatrix} \overline{i}&\overline{j}&\overline{k}\\ 2&7&-1\\ 4&-9&-2 \end{vmatrix} = -23\overline{i} - 0\overline{j} - 46\overline{k}$ ,

и канонические уравнения станут:

${x - 2\over{-23}} = {y - 0\over{0}} = {z - 0\over{-46}}\arrowvert * (-23)\to{x - 1\over{1}} = {y\over{0}} = {z\over{2}}.$

Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых

Угол между двумя прямыми $(\varphi)$ :

${x - x_{1}\over{l_{1}}} = {y - y_{1}\over{m_{1}}} = {z - z_{1}\over{p_{1}}}$ и ${x - x_{2}\over{l_{2}}} = {y - y_{2}\over{m_{2}}} = {z - z_{2}\over{p_{2}}}$

равен углу между их направляющими векторами $\overline{S_{1}} = (l_{1}, m_{1}, p_{1})$ и $\overline{S_{2}} = (l_{2}, m_{2}, p_{2})$ , поэтому

${cos\varphi = cos(\overline{S}_{1}}, \overline{S}_{2}})$ = ${l_{1}l_{2} + m_{1}m_{2} + p_{1}p_{2}}\over{\sqrt{l_{1}^2 + m_{1}^2 + p_{1}^2}} * {\sqrt{l_{2}^2 + m_{2}^2 + p_{2}^2}}$

(5)

Условия параллельности и перпендикулярности прямых соответственно запишутся:

${l_{1}\over{l_{2}}} = {m_{1}\over{m_{2}}} = {p_{1}\over{p_{2}}}$ и $l_{1}l_{2} + m_{1}m_{2} + p_{1}p_{2} = 0$ .

(6)

Примеры решения задач

Давайте рассмотрим первый пример, где можно двумя способами построить прямую:

[stextbox id=”warning” caption=”Пример 1″]

Задача

При точке $M (1, 5, 2)$ и направляющем векторе $\overline{S} = (3, 0, 4)$ необходимо:

составить каноническое уравнение прямой;
построить эту прямую.

Решение

1) По формуле (1) запишем каноническое уравнение прямой $l$ :

${x - 1\over{3}} = {y - 5\over{0}} = {z - 2\over{4}}$ = $(t)$ .

2) Рассмотрим два способа построения прямой $l$ .

Первый способ

В системе координат $XYZ$ строим вектор $\overline{S} = (3, 0, 4)$ и точку $M (1, 5, 2)$ и проводим через точку $M$ прямую параллельную вектору $\overline{S}$ .

Второй способ

По формуле (2) запишем каноническое уравнение прямой в параметрическом виде:

$\left\{\begin{aligned} x = 3t + 1\\ y = 0 * t + 5\\ z = 4t + 2 \end{aligned} \right$

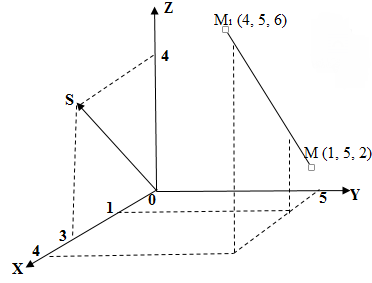
Уравнение прямой

На рисунке видно, что при произвольных значениях $t$ из системы находим координаты соответствующих точек, которые принадлежат прямой $l$ . Так при $t = 1$ находим координаты $M_{1}(4, 5, 6)$ . Через две точки $M$ и $M_{1}$ проводим прямую $l$ .

[/stextbox]

Очевидно, что найти острый угол между прямыми совершенно не сложно при знании темы и определённых формул. Давайте разберём такой пример:

[stextbox id=”warning” caption=”Пример 2″]

Задача

Найти острый угол между прямыми:

${x - 4\over{6}} = {y + 2\over{-2}} = {z\over{3}}$ , ${x + {2}\over{-2}} = {y - {5}\over{-1}} = {z + 1\over{-2}}$

(7)

Решение

По формуле (7) получаем:

$cos\theta$ = ${6 * (-2) + (-2)(-1) + 3 * (-2)}\over{\sqrt{6^2 + (-2)^2 + 3^2} * \sqrt{(-2)^2 + (-1)^2 + (-2)^2}$ = ${-12 +2 -6\over{7 * 3}}$ = $-{16\over21}.$

Так как $cos\theta = -{16\over{21}} < 0$ , тогда угол $\theta$ тупой, $\theta = arccos (-{16\over{21}}$ , а острый угол $\varphi = 180^0 - \theta$ .

Ответ

$\varphi = arccos{16\over{21}}$ .

[/stextbox]

Рассмотрим последний пример, где нужно составить уравнение. Здесь, как и в каждой задаче, важно знать и понимать, какой формулой нужно воспользоваться.

[stextbox id=”warning” caption=”Пример 3″]

Задача

Составить уравнение прямой $l$ , которая проходит через точку $M(2, -4, 3)$ и параллельна прямой $x = -5t + 4, y = 2t, z = 8t - 5$ .

Решение

От параметрического уравнения переходим к каноническому ${x - 4\over{(-5)}} = {y\over{2}} = {z + 5\over{8}}\to\overline{S} = (-5, 2, 8)$ При условии параллельности прямых $\overline{S}||\overline{S_{1}}$ то есть направляющим вектором новой прямой может служить известный вектор $\overline{S} = (-5, 2, 8)$ и по формуле (1) у нас получается:

${x - 2\over{-5}} = {y - 4\over{2}} = {z - 3\over{8}}$ .

Ответ

${x - 2\over{-5}} = {y - 4\over{2}} = {z - 3\over{8}}$ .

[/stextbox]

Нашли ошибку? Выделите текст и нажмите CTRL + Enter

сагдиана на Решить уравнение с дробями онлайнничего не понятно!
акмарал на Более 50 основных формул по физике с пояснениема эти формулы обычно используют в олимпиядах
всем пока на Решить уравнение с дробями онлайнничего не понятно. калькулятор не работает.
Великий гей Никола Тесла на Более 50 основных формул по физике с пояснениемСайт параша, я пытался списать ЕГЭ по физике с помощью них, я блять сдал его на 99999 балов, и теперь
некто на Примеры решения матриц с ответамиНеправильные ответы, учите матрицу гении

Прямая в пространстве – виды уравнения прямой в пространстве

Параметрическое и каноническое уравнение прямой в пространстве

Уравнение прямой в пространстве, которая проходит через две заданные точки

Общее уравнение прямой – переход к каноническому уравнению

Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых

Примеры решения задач

Авторизуйтесь