Ellips

О чем статья

Что такое эллипс и фокусное расстояние

Эллипс — это множество точек плоскости, сумма расстояний которых от двух заданных точек, что называются фокусами, есть постоянная величина и равна $2a\quad{(a > 0)}$ .

Обозначим фокусы эллипса $F_{1}$ и $F_{2}$ . Допустим, что расстояние $F_{1}{F_{2}}$ = $2c$ — фокусное расстояние.

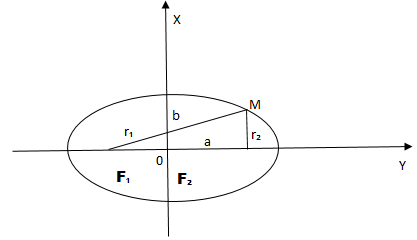
Эллипс

Рис. 1

$F_{1}, F_{2}$ – фокусы .

$F_{1} = (c, 0)$ ; $F_{2} = (- c ; 0)$ ,

$c$ – половина расстояния между фокусами;

$a$ – большая полуось;

$b$ – малая полуось.

Теорема:

Фокусное расстояние и полуоси связаны соотношением:

$a^2 = b^2 + c^2$

Если точка $M$ находится на пересечении эллипса с вертикальной осью, $r_{1} + r_{2} = 2 * \sqrt{b^2 + c^2}$ (теорема Пифагора). Если же точка $M$ находится на пересечении его с горизонтальной осью, $r_1} + r_{2} = a - c + a + c$ . Так как по определению сумма $r_{1} + r_2}$ — постоянная величина, то приравнивая получается:

$a^2 = b^2 + c^2\to{r_{1} + r_{2} = 2a$ .

Уравнение эллипса

Уравнение элиппса бывает двух видов:

Каноническое уравнение эллипса.
Параметрическое уравнение эллипса.

Сначала рассмотрим каноническое уравнение эллипса:

Уравнение описывает эллипс в декартовой системе координат. Если центр эллипсa $O$ в начале системы координат, а большая ось лежит на абсциссе, то эллипс описывается уравнением:

$1 = {x^2\over{a^2}} + {y^2\over{b^2}}$

Если центр эллипсa $O$ смещен в точку с координатами $(x_{0}, y_{0})$ тогда уравнение:

$1 = {(x - x_{0})^2\over{a^2}} + {(y - y_{0})^2\over{b^2}}$

Чтобы получить каноническое уравнение эллипса, разместим $F_{1}$ и $F_{2}$ на оси $OX$ симметричной к началу координат. Тогда у фокусов будут такие координаты $F_{2}(-c, 0)$ и $F_{2}(c, 0)$ (см. рис. 2).

Пусть $M(x, y)$ — произвольная точка эллипса. Обозначим через $r_{2}$ и $r_{1}$ — расстояние от точки $M$ к фокусам. Согласно с определением эллипса:

$r_{1} + r_{2} = 2a$

(1)

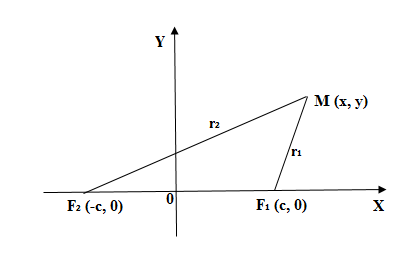
Уравнение эллипса

Рис. 2

Подставим в (1) $r_{1} = F_{1}M = \sqrt{(x - c)^2 + (y - 0)^2}$ , $r_{2} = \sqrt{(x + c)^2 + y^2}$ и освободимся от иррациональности, подняв обе части к квадрату, получим:

$r_{2} = 2a - r_{1}\to\sqrt{(x + c)^2 + y^2} = 2a - \sqrt{(x - c)^2 + y^2}}\to{x^2 + 2cx + c^2 + y^2} = 4a^2 - 4a\sqrt{(x - c)^2) + y^2} + x^2 - 2cx + c^2 + y^2\to{4a}\sqrt{(x - c^2 + y^2} = 4a^2 - 4cx\arrowvert:4$

$a\sqrt{(x - c)^2 + y^2} =a^2 - cx$

(подносим к квадрату обе части): $\to{a^2x^2 - 2ca^2x + a^2c^2 + a^2y^2} = {a^4 - 2ca^2x + c^2x^2\to{(a^2 - c^2)x^2 + a^2y^2 = a^2(a^2 - c^2)\arrowvert:a^2(a^2 - c^2)$ ,

${x^2\over{a^2}} + {y^2\over{a^2 - c^2}} = 1$

Обозначим: $a^2 - c^2 = b^2$ , получаем каноническое уравнение эллипса:

${x^2\over{a^2}} + {y^2\over{b^2}} = {1}$

(2)

Отметим, что по известному свойству треугольника (сумма двух сторон больше третьей) из $\Delta{F_{1}}MF_{2}$ у нас получается $F_{2}M + F_{1}M > F_{1}F_{2}\to{r_{1} + r_{2}} > 2c$ . Так как $r_{1} + r_{2} = 2a$ , тогда $2a > 2c\to{a >c}$ , и поэтому $b^2 = a^2 - c^2 >0$ .

Для построения эллипса обратим внимание, что если точка $M_{1}(x, y)$ принадлежит эллипсу, то есть удовлетворяет уравнение (2), тогда точки $M_{2}(-x, y), M_{3}(-x, -y), M_{4}(x, -y)$ тоже удовлетворяют это уравнение: из

${x^2\over{a^2}} + {y^2\over{b^2}} = 1\to{(\pm{x})^2\over{a^2}} + {(\pm{y})^2\over{b^2}} = {1}$ .

Точки $M_{1}, M_{2}, M_{3}, M_{4}$ — расположены симметрично относительно осей координат. Значит, эллипс — фигура, симметричная относительно координатных осей. Поэтому достаточно построить график в первой четверти, а тогда симметрично продолжить его.

Из уравнения (2) находим $y = \pm{{b}\over{a}}\sqrt{a^2 - x^2$ , для первой четверти ${y} = {b\over{a}}\sqrt{a^2 - x^2}$ .

Если $y = 0$ , тогда $x = a$ . Если же $x = 0$ , тогда $y = b$ . Точки $A_{1}(a, 0)$ и $B_{1}(0, b)$ , а также симметричные с ними $A_{2}(-a, 0)$ , $B_{2}(0, -b)$ — вершины эллипса, точка $O(0, 0)$ — центр эллипса, $A_{1}A_{2}$ = $2a$ большая ось, $B_{1}B_{2} = 2b$ — малая ось эллипса.

Если $M\in$ первой четверти, тогда из $y = {b\over{a}}\sqrt{a^2 - x^2$ получается, что при возрастании $x$ от $0$ к $a$ значение $y$ падает от $b$ к $0$ . (рис. 3)

Параметрическое уравнение выглядит так:

$\left\{ \begin{aligned} x = a{cos}\alpha\\ y = b{sin}\alpha \end{aligned}\quad {0\leq\alpha < 2\pi \right$

Основные свойства эллипса

Рассмотрим основные свойства эллипса, которые необходимы для решения многих задач.

1. Угол между касательной к эллипсу и фокальным радиусом $r_{1}$ равен углу между касательной и фокальным радиусом $r_{2}$ .

2. Уравнение касательной к эллипсу в точке $M$ с координатами $(x_{M}, y_{M})$ :

$1 = {x x_{M}\over{a^{2}}} + {y y_{M}\over{b^{2}}}$ .

3. Если эллипс пересекается двумя параллельными прямыми, то отрезок, который соединяет середины отрезков образовавшихся при пересечении прямых и эллипса, всегда проходит через середину (центр) эллипсa. (При помощи данного свойства можно построить эллипс при помощи циркуля и линейка, а также найти центр эллипса).

4. Эволюта эллипсa — это астероида, которая растянута вдоль короткой оси.

5. Если вписать эллипс с фокусами $F_{1}$ и $F_{2}$ у треугольника $ABC$ , тогда выполняется соотношение:

${1}$ = ${{\overline{F_{1}A} * \overline{F_{2}A}}\over{\overline{CA} * \overline{AB}}} + {{\overline{F_{1}B} * \overline{F_{2}B}}\over{\overline{AB} * \overline{BC}}} + {{\overline{F_{1}C} * \overline{F_{2}C}}\over{\overline{BC} * \overline{CA}}}$

Эксцентриситет эллипса

[stextbox id=»info» defcaption=»true»]Эксентриситет эллипса — это величина отношения межфокусного расстояния к большей оси и после сокращения на $2$ обозначается $\varepsilon = {c\over{a}}$ [/stextbox]

Значения эксентриситета характеризует степень «сплющенность» эллипса. Если $a = b =R$ , тогда $c = {\sqrt{a^2 + b^2}} = 0\to{\varepsilon = 0}$ — получается круг. Если же $b = 0$ , тогда $\varepsilon = 1$ — эллипс превращается в отрезок. В некоторых случаях $0 < \varepsilon < 1$ . Для фокальных радиусов приведём без доказательства такие формулы:

$\left\{ \begin{aligned} r_{1} = a - \varepsilon{x},\\ r_{2} = a + \varepsilon, \end{aligned} \quad{x\in[-a, a]. \right$

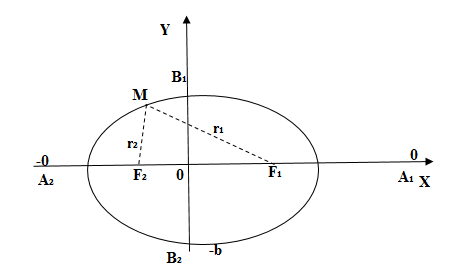
Эксцентриситет

Рис. 3

Эллипс можно построить механическим способом. Из канонического уравнения нужно найти полуоси $a$ и $b$ , тогда вычислим $c = {\sqrt{a^2 + b^2}}$ — полуфокусное расстояние.

Строим фокусы $F_{1}$ и $F_{2}$ на расстоянии один от другого $2c$ Концы не растянутой нити длиной $2a$ закрепляем в точках $F_{1}$ и $F_{2}$ . Натягивая остриём карандаша нитку, водим остриём по плоскости таким образом, чтобы нитка скользила по острию. Карандаш при этом опишет полуось. Оттягивая нить в противоположную сторону, начертим вторую половину эллипса.

Примеры решения задач

[stextbox id=»warning» caption=»Пример 1″]

Задача

Задан эллипс уравнением ${x^2\over{25}} + {y^2\over{9}} = 1$ и точки $M_{0}(4; 1,8), M_{1}(3; 2,4)$ . Необходимо:

убедиться, что точки $M_{0}$ и $M_{1}$ лежат на эллипсе;
найти полуоси эллипса и координаты его фокусов;
найти расстояние от точки $M_{0}$ к фокусам;
убедиться, что сумма этих расстояний равна длине большой оси;
найти эксентриситет эллипса.

Решение

1. Подставим координаты $x = 4 y = 1,8$ точки $M_{0}$ в левую часть уравнения эллипса:

${x^2\over{25}} + {y^2\over{9}} = {4^2\over25}} + {1,8 * 1,8\over{9}} = {16\over25}} + {36\over{100}} = {16\over{25}} + {9\over25}} = 1$ — точка $M_{0}$ лежит на эллипсе. Аналогично для $M_{1}(3; 2,4)$ :

${9\over{25}} + {2*4 * 2,4\over{9}} = {9\over{25}} + 0,64 = {9\over{25}} + {64\over{100}} = {9 + 16\over{25}} = 1$ точка $M_{1}$ лежит на эллипсе.

2. С канонического ${x^2\over{a^2}} + {y^2\over{b^2}} = {1}$ и данного уравнения ${x^2\over{25}} + {y^2\over{9}} = 1$ эллипса выходит: $a^2 = {25},\quad{b^2 = 9}\to{a = 5, b = 3}.$ Из равенства $b^2 = a^2 - c^2 > 0$ получается:

$b^2 = a^2 - c^2\to {c^2 = a^2 - b^2 = 25 - 9} = {16}\to{c = 4}$ — полуфокусное расстояние. Координаты фокусов $F_{1}(4; 0)$ и $F_{2}(-4; 0)$ .

3. Найдём фокальные радиусы точки $M_{0}$ :

$r_{2} = F_{2}M_{0} = \sqrt{(4 - (-4))^2 + 1,8^2} = \sqrt{64 + 3,24} = \sqrt{67,24} = 8,2$

$r_{1} = F_{1}M_{0} = \sqrt{(4 - 4)^2 + 1,8^2} = 1,8.$

4. Найдём сумму $r_{1} + r_{2} = 1, 8 + 8.2 = 10 = 2 * 5 = 2a$ , что отвечает определению эллипса.

5. Эксцентриситет находится по формуле $\varepsilon = {c\over{a}} = {4\over{5}} = 0.8$ .

[/stextbox]

[stextbox id=»warning» caption=»Пример 2″]

Задача

Найти оси, вершины и фокусы эллипса $169x^2 + 25y^2 - 4225 = 0$

Решение

Сведём обычное уравнение к каноническому:

$169x^2 + 25y^2 - 4225 = 0\to{x^2\over{25}} + {y^2\over{169}} = 1$

$a^2 = 25$ , $b^2 = 169\to{a = 5, b = 13}$ . Вершины эллипса в точках $A_{1}(5, 0)$ , $B_{1}(0, 13)$ , $A_{2}(-5, 0)$ , $B_{2}(0, -13)$ . Строим вершины на координатных осях и соединяем плавной линией (см. рис. 2). Так как в данном случае $b = 13$ больше, чем $a = 5$ , то эллипс, который вытянут вдоль оси $OY$ , находим полуфокусное расстояние $c = \sqrt{b^2 - a^2} = \sqrt{169 - 25} = \sqrt{144} = 12$ .

Фокусы в точках $F_{1}(0, 12)$ и $F_{2}(0, -12)$ . (см. рис. 3)

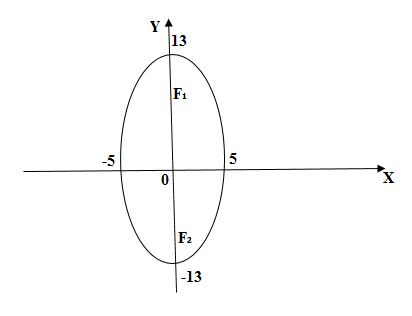
Уравнение эллипса

Рис. 4

[/stextbox]

[stextbox id=»warning» caption=»Пример 3″]

Найти оси, вершины и фокусы эллипса $25x^2 + 144y^2 = 3600\quad{:}\arrowvert\to{25x^2\over{3600}} + {144y^2\over{3600}} = {1}\to{x^2\over{144}} + {y^2\over{25}} = {1}$ или ${X^2\over{12^2}} + {y^2\over{5^2}} = {1}$ . Построить эллипс.

Сравнивая последнее уравнение с уравнением (2), у нас получается:

$a^2 = 12^2$ , $b^2 = 5^2\to{a = 12, b = 5}$ . Откуда находим оси эллипса: $2a = 24$ , $2b = 10$ и координаты вершин: $A_{1}(12, 0)$ , $A_{2} (-12, 0)$ , $B_{1}(0, 5)$ , $B_{2}(0, -5)$ . Дальше из формулы:

$b^2 = a^2 - c^2\to{c^2 = a^2 - b^2 = 144 - 25 = 119}\to{c = \sqrt{119}}\approx{10,91}$ . Значит, фокусами эллипса есть точки: $F_{1}(\sqrt{119}, 0)$ и $F_{2}(-\sqrt{119}, 0)$ . Для построения эллипса отложим на осях $OX$ и $OY$ вершины $A_{1}, B_{1}, A_{2}, B_{2}$ соответственно соединим их плавной линией, (см. задачу 1).

Замечание! Если в каноническом уравнении ${x^2\over{a^2}} + {y^2\over{b^2}} = {1}$ большей полуосью будет $b > a$ , тогда фокусы эллипса будут расположены на оси $OY$ и тогда $c = \sqrt{b^2 - a^2}$ .

[/stextbox]

Нашли ошибку? Выделите текст и нажмите CTRL + Enter

сагдиана на Решить уравнение с дробями онлайнничего не понятно!
акмарал на Более 50 основных формул по физике с пояснениема эти формулы обычно используют в олимпиядах
всем пока на Решить уравнение с дробями онлайнничего не понятно. калькулятор не работает.
Великий гей Никола Тесла на Более 50 основных формул по физике с пояснениемСайт параша, я пытался списать ЕГЭ по физике с помощью них, я блять сдал его на 99999 балов, и теперь
некто на Примеры решения матриц с ответамиНеправильные ответы, учите матрицу гении

Ellips

Что такое эллипс и фокусное расстояние

Уравнение эллипса

Основные свойства эллипса

Эксцентриситет эллипса

Примеры решения задач

Авторизуйтесь