Поверхности вращения, цилиндрические и канонические поверхности

Рассмотрим поверхности, которые задаются уравнением второго порядка. Это цилиндрические поверхности, канонические и поверхности вращения.

О чем статья

Цилиндрическая поверхность

[stextbox id=»info» defcaption=»true»]

Цилиндрическая поверхность — это поверхность, которая образована прямыми, — образующими, параллельными заданной прямой $l$ и они пересекают данную кривую линию $L$ — направляющую (см. рис. 1).

[/stextbox]

Цилиндрическая поверхность

Рис. 1

В общем случае уравнение цилиндрической поверхности записывается $F (x, y, z) = 0$ .

В отдельных случаях, когда образующие цилиндрические поверхности параллельны одной из координатных осей, тогда у уравнения цилиндрической поверхности есть только две переменные. Причём, образующие цилиндрические поверхности параллельны той координатной оси, переменная которой в уравнении отсутствует:

$F_{1}(x, y) = 0$ — цилиндрическая поверхность с образующими $||OZ$ ;

$F_{2}(x, z) = 0$ — цилиндрическая поверхность с образующими $||OY$ ;

$F_{3}(y, z) = 0$ — цилиндрическая поверхность с образующими $||OX$ .

Канонические поверхности

[stextbox id=»info» defcaption=»true»]Канонические поверхности — это поверхности, которые образованы прямыми, образующими конуса, и которые проходят через данную точку — вершину конуса, — и пересекают данную кривую линию — направляющую конуса.[/stextbox]

Допустим, ${x^2\over{a^2}} + {z^2\over{c^2}} = {y^2}$ — эллиптический конус (см. рис. 2), ось $OY$ — ось симметрии, вершина в точке $O(0, 0, 0)$ за направляющую можно взять линию ${x^2\over{a^2}} + {z^2\over{c^2}} = {1}$ — эллипс в плоскости $y = 1$ .

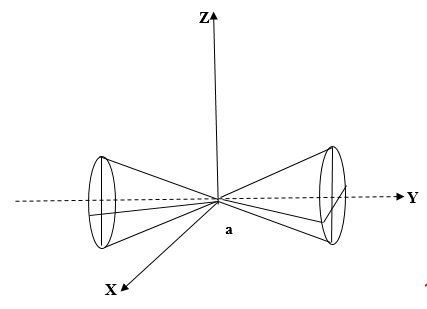
канонические поверхности

Рис. 2

Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.

Подробнее

Поверхности вращения

Пусть в плоскости $YOZ$ задана линия $L$ уравнением $F(y, z) = 0$ . Чтобы получить поверхность вращения линии $L$ вокруг, например, оси $OY$ необходимо вместо переменной $Z$ поставить в уравнение $F (y, z) = 0$ выражение $\pm\sqrt{x^2 + z^2}$ . Уравнение $F (y, \pm\sqrt{x^2 + z^2}) = 0$ описывает поверхность вращения линии $L$ вокруг оси $OY$ (см. рис. 3).

Поверхности вращения

Рис. 3

Поверхности второго порядка и их уравнения

Рассмотрим поверхности второго порядка и какие у них уравнения, которые считаются основными для решения задач:

1. Сфера — $x^2 + y^2 + z^2 = R^2$ :

zПоверхности второго порядка - сфера

2. Эллипсоид — ${x^2\over{a^2}} + {y^2\over{b^2}} + {z^2\over{c^2}} = {1}$ :

Поверхности второго порядка

3. Однополостный гиперболоид — ${x^2\over{a^2}} + {y^2\over{b^2}} - {z^2\over{c^2}} = {1}$ :

Поверхности второго порядка

4. Двуполостный гиперболоид — ${x^2\over{a^2}} + {y^2\over{b^2}} - {z^2\over{c^2}} = {-1}$ :

Поверхности второго порядка - гиперболоид

5. Гиперболический параболоид — ${x^2\over{p}} - {y^2\over{q}} = {2z}$ :

Поверхности второго порядка - параболоид

6. Конус — $z^2 = x^2 + y^2$ :

konus

7. Эллиптический параболоид — ${x^2\over{a^2}} + {y^2\over{b^2}} = {z}$

Поверхности второго порядка - эллиптический параболод

Примеры решения задач

[stextbox id=»warning» caption=»Пример 1″]

Задача

Составить уравнение цилиндрической поверхности, у которой направляющая лежит в плоскости $xOy$ и имеет уравнение $x^2 + y^2 = 4$ , а образующие параллельны вектору $\overline{a} = (0; 1; 1)$ .

Решение

Согласно условию задачи $F(x, y) = x^2 + y^2 = 4$ и $\alpha = 0, \beta = 1, \gamma = 1$ тогда, по формуле $F ({x - z}{\alpha\over\gamma}; {y - z}{\beta\over\gamma}) = 0$ у уравнения данной цилиндрической поверхности будет такой вид:

$(x - z {0\over{1}})^2 + (y - z{1\over{1}})^2 - 4 = 0$

В итоге получается:

$x^2 + (y - z)^2 - 4 = 0$

Ответ

Уравнение цилиндрической поверхности имеет такой вид: $x^2 + (y - z)^2 - 4 = 0$

[/stextbox]

[stextbox id=»warning» caption=»Пример 2″]

Задача

Определить вид поверхности $3x^2 + 6y^2 - 24 = 0$ .

Решение

Необходимо данное уравнение привести к соответствующему виду:

${x^2\over{8}} + {y^2\over{4}} = 1$

Это уравнение в пространстве определяет эллиптическую цилиндрическую поверхность с направляющей в плоскости $xOy$ и образующими, параллельными оси $Oz$ .

Ответ

Уравнение $3x^2 + 6y^2 - 24 = 0$ определяет эллиптическую цилиндрическую поверхность.

[/stextbox]

[stextbox id=»warning» caption=»Пример 3″]

Задача

Составить уравнение конической поверхности с вершиной в точке $(0, 0, c)$ , $c > 0$ и направляющей.

${x^2\over{a^2}} + {y^2\over{b^2}} = {1}$ .

Решение

У данной конической поверхности такое уравнение:

${1\over{a^2}}({cx\over{c - z}})^2 + {1\over{b^2}}({cy\over{c - z}})^2 = {1}$

После определённых преобразований у нас получается:

${x^2\over{a^2}} + {y^2\over{b^2}} = {(z - c)^2\over{c^2}}$

Ответ

Уравнение конической поверхности — ${x^2\over{a^2}} + {y^2\over{b^2}} = {(z - c)^2\over{c^2}}$ .

[/stextbox]

Как видите, в любой задаче большую роль играют формулы, которые необходимо применять во время решения. Только тогда вы достигнете хороших результатов.

Нашли ошибку? Выделите текст и нажмите CTRL + Enter

сагдиана на Решить уравнение с дробями онлайнничего не понятно!
акмарал на Более 50 основных формул по физике с пояснениема эти формулы обычно используют в олимпиядах
всем пока на Решить уравнение с дробями онлайнничего не понятно. калькулятор не работает.
Великий гей Никола Тесла на Более 50 основных формул по физике с пояснениемСайт параша, я пытался списать ЕГЭ по физике с помощью них, я блять сдал его на 99999 балов, и теперь
некто на Примеры решения матриц с ответамиНеправильные ответы, учите матрицу гении

Поверхности вращения, цилиндрические и канонические поверхности

Цилиндрическая поверхность

Канонические поверхности

Поверхности вращения

Поверхности второго порядка и их уравнения

Примеры решения задач

Авторизуйтесь