Уравнение плоскости

О чем статья

Уравнение плоскости через точку и нормальный вектор. Общее уравнение плоскости

Рассмотрим уравнение плоскости через точку на примере, так как будет более понятно, чем определения и термины.

Пусть в пространстве задана точка $M_{1}(x_{1}, y_{1}, z_{1})$ и ненулевой вектор $\overline{n} = (A, B, C)$ . Через точку $M_{1}$ можно провести единственную плоскость $P$ перпендикулярно вектору $\overline{n}$ . Чтобы получить уравнение плоскости, выберем на ней произвольную точку $M (x, y, z)$ и рассмотрим вектор $\overline{M_{1}M} = (x - x_{1}, y - y_{1}, z - z_{1})$ (см. рис. 1)

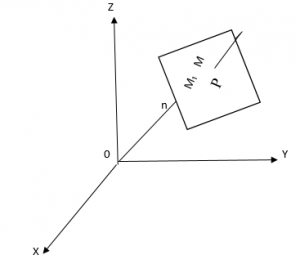
Графическое изображение - плоскость в пространстве

Рис. 1

[stextbox id=”info” defcaption=”true”]

Точка $M\in{P}$ тогда и только тогда, когда

$\overline{M_{1}M}\perp\overline{n}\to\overline{M_{1}M} * \overline{n}$ = $0\to$

${A(x - x_{1}) + B(y - y_{1}) + C(z - z_{1}) = 0$

(1)

– уравнение плоскости, которая проходит через данную точку с нормальным вектором.

[/stextbox]

Открыв скобки в (1) у нас получается:

$Ax + By + Cz + D = 0$

(2}

– это общее уравнение плоскости, где обозначено: $\overline{D} = -Ax_{1} - By_{1} - Cz_{1}$ .

Значит, плоскости $P$ отвечает линейное уравнение (2). Наоборот, если задано линейное уравнение вида (2), тогда нетрудно найти точку $M_{1}(x_{1}, y_{1}, z_{1})$ , координаты которой удовлетворяют это уравнение, и записать вектор $\overline{n} = (A, B, C).$ Вектор $\overline{n}$ и точка определяют плоскость $P$ .

Исследование общего уравнения плоскостей

Рассматриваются частные случаи размещения плоскостей:

$Ax + By + Cz + D = 0$

когда некоторые из чисел $A, B, C, D$ равняются нулю.

1. Если $D = 0$ , тогда уравнение выглядит так: $Ax + By + Cz = 0$ , плоскость проходит через начало координат $O(0, 0, 0)$ перпендикулярно вектору $\overline{n} = (A, B, C)$ .

2. Если $A = 0$ , тогда у нас получается уравнение $By + Cz + D = 0$ , вектор $\overline{n} = (0, B, C)$ принадлежит плоскости $YOZ$ . Так как плоскость $P\perp{YOZ}$ , или же $P||OX$ (см. рис. 2). Уравнения плоскости $By + Cz + D = 0$ – это уравнение следа в плоскости $YOZ$ .

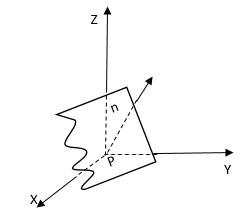
Общее уравнение плоскости

Рис. 2

3. Если же $A = D = 0$ , тогда плоскость $By + Cz = 0$ проходит через ось $OX$ .

4. Если же $B = 0$ , тогда уравнение плоскости выглядит так: $Ax + Cz + D = 0$ , $\overline{n} = (A, O, C)$ принадлежит плоскости $XOZ$ . Плоскость $P\perp\overline{n}\to P\perp XOZ\Longleftrightarrow{P}||OY$ (см. рис. 3)

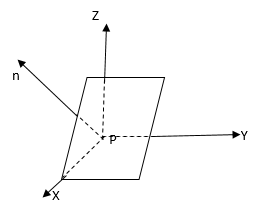
Уравнение плоскости

Рис. 3

5. Если же $B = D = 0$ , тогда плоскость $Ax + Cz = 0$ проходит через всю ось $OY$ .

6. Если $C = 0$ , тогда получается уравнение $Ax + By + D = 0$ , $\overline{n} = (A, B, C)\in{XOY}\toP\perp{XOY}$ , или $P||{OZ}$ .

7. Если же $C = D = 0$ , тогда плоскость $Ax + By = 0$ проходит через ось $OZ$ .

Вывод:

На основании 2, 4 и 6 получается, что плоскость параллельна той координатной оси, переменная которой в уравнении отсутствует.

8. $A = B = 0$ , плоскость $Cz + D = 0\to{z} = -{D\over{C}}$ , либо же $z = c$ , где $c = -{D\over{C}}$ . Вектор $\overline{n}$ = $(0, 0, C)$ направленный вдоль оси $OZ$ , поэтому плоскость перпендикулярна к оси $OZ$ в точке $(0, 0, c)$

В частности, если $C = 0$ , тогда $Z = 0$ – уравнение координатной плоскости $XOY$ .

9. Если $A = C = 0$ , тогда у нас есть плоскость $By + D = 0$ , либо $y = b$ , где $b = -{D\over{B}}$ . Вектор $\overline{n} = (0, B, 0)$ направляющий вдоль оси $OY$ . Плоскость перпендикулярна оси $OY$ в точке $(0, b, 0)$ .

В частности, если $b = 0$ , тогда $y = 0$ – уравнение координатной плоскости $XOZ$ .

10. На конец, если $B = C = 0$ , тогда $Ax + D = 0\to{x = a$ , где $a = -{D\over{A}}, P\perp{OX}$

При $a = 0$ получается $x = 0$ – уравнение координатной плоскости $YOZ$ .

Нужна помощь в написании работы?

Мы - биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Уравнение плоскости в отрезках

Прежде чем записывать уравнение плоскости в отрезках, вспомним общее уравнение:

$Ax + By + Cz + D = 0$

если ни одно из чисел $A, B, C, D$ не равняется нулю, тогда плоскость можно построить за тремя точками пересечения её с координатными осями:

$M_{1}(a, 0, 0)$ , $M_{2}(0, b, 0)$ , $M_{3}(0, 0, c)$ , где $a = -{D\over{A}}$ , $b = -{D\over{B}}$ , $c = -{D\over{C}}$ – отрезки, которые отсекают плоскость на координатных осях (см. рис. 4)

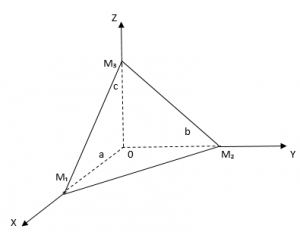
Графическое изображение - уравнение плоскости в отрезках

Рис. 4

Уравнение плоскости в отрезках запишется:

${x\over{a}} + {y\over{b}} + {z\over{c}} = l$

(3)

[stextbox id=”info” defcaption=”true”] Прямые $M_{1}M_{2}$ , $M_{2}M_{3}$ , $M_{1}M_{3}$ называются следами данной плоскости на координатных плоскостях $XOY$ , $YOZ$ , $XOZ$ – соответственно. Их уравнения можно получить из общего, если в последнем приравнять к нулю соответствующую переменную.[/stextbox] Так, например, если $z = 0$ плоскость $(XOY)$ , тогда в этой плоскости уравнения следа $M_{1}M_{2}$ запишется:

$AX + By + D = 0$

Аналогично и до остальных следов.

Уравнение плоскости проходящей через три точки

Пусть заданы три точки $M_{1} (x_{1}, y_{1}, z_{1}), M_{2}(x_{2}, y_{2}, z_{2}), M_{3}(x_{3}, y_{3}, z_{3})$ , которые не лежат на одной линии. Произвольная точка $M(x, y, z)$ отлична от $M_{1}, M_{2}, M_{3}$ , будет находиться в плоскости точек $M_{1}, M_{2}, M_{3}$ тогда, и только тогда, когда векторы $\overline{M_{1}M}$ = $(x - x_{1}, y - y_{1}, z - z_{1})$ , $\overline{M_{1}M_{2}} = (x_{2} - x_{1}, y_{2} - y_{1}, z_{2} - z_{1}), \overline{M_{1}M_{3}} = (x_{3} - x_{1}, y_{3} - y_{1}, z_{3} - z_{1})$

компланарные, то есть их смешанное произведение $(\overline{M_{1}M}$ x $\overline{M_{1}M_{2}})\overline{M_{1}M_{3}} = 0$

В координатной форме запишется:

$\begin{vmatrix} x - x_{1}&y - y_{1}&z - z_{1}\\ x_{2} - x_{1}&y_{2} - y_{1}&z_{2} - z_{1}\\ x_{3} - x_{1}&y_{3} - y_{1}&z_{3} - z_{1} \end{vmatrix} = 0 \right$

(4)

– уравнение плоскости проходящее через три точки.

Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей

Если для однозначности угол между двумя плоскостями называть один из меньших двугранных углов между ними, а соответственно к этому самый маленький из углов назовём углом между двумя векторами, тогда между двумя плоскостями есть угол между их нормальными векторами.

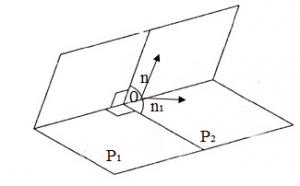
Угол между двумя плоскостями

Рис. 5

$cos\theta$ = ${\overline{n_{1}}}{\overline{n_{2}}}\over{\overline{|n_1|}\overline{|n_{2|}}$ = $A_{1}A_{2} + B_{1}B_{2} + C_{1}C_{2}\over{\sqrt{A_{1}^2 + B_{1}^2 + C_{1}^2} * \sqrt{A_{2}^2 + B_{2}^2 + C_{2}^2}$ ,

(5)

где $\overline{n_{1}}(A_{1}, B_{1}, C_{1}})$ , $\overline{{n_2}}(A_{2}, B_{2}, C_{2})$ – нормальные векторы плоскости

$A_{1}x + B_{1}y + C_{1}z + D = 0$ – $(P_{1})$ ,

$A_{2}x + B_{2}y + C_{2}z + D_{2} = 0$ – $P_{2}$ .

Если $P_{1}\perp{P_{2}}$ , тогда $\theta = 90^0, cos\theta$ = $0$

И тогда:

$A_{1}A_{2} + B_{1}B_{2} + C_{1}C_{2} = 0$

(6)

– условие перпендикулярности двух плоскостей.

Когда же $P_{1}||{P_{2}}$ , тогда получим:

$A_{1}\over{A_{2}}$ = $B_{1}\over{B_{2}}$ = $C_{1}\over{C_{2}}$

(7)

– условие параллельности двух плоскостей.

Расстояние от точки до плоскости

Расстояние от точки до плоскости рассмотрим при помощи примера, формул и рисунка.

Расстояние $d$ от точки $M_{0}(x_{0}, y_{0}, z_{0})$ до плоскости $P: Ax + By + Cz + D = 0$ , выражается формулой:

$d$ = $|Ax_{0} + By_{0} + Cz_{0} + D|\over{\sqrt{A^2 + B^2 + C^2}}$

(8)

Действительно, на рисунке 6:

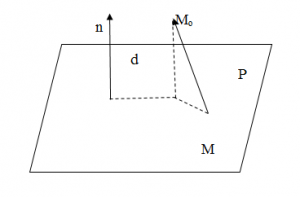
Расстояние от точки до плоскости

Рис. 6

видим, что для произвольной точки $M(x, y, z)\in{P}$

$d$ = $|{pr_\overline{n}}{\overline{MM_{0}}}$ = $|\overline{n} * \overline{MM_{0}}|\over{\overline{n}}$ ,

где $\overline{MM_{0}} = (x_{0} - x, y_{0} - y, z_{0} - z)$ , $\overline{n} = (A, B, C)$ .

Так как $\overline{n} * \overline{MM_{0}}$ = $A(x_{0} - x) + B(y_{0} - y) + C{z_{0} - z)$ = $Ax_{0} + By_{0} + Cz_{0} + (-Ax - By - Cz)$ = $Ax_{0} + By_{0} + Cz_{0} + D$ ,

потому что $Ax + By + Cz + D = 0\to{D} = - Ax - By - Cz$ , а $\overline{|n|} = \sqrt{A^2 + B^2 + C^2}$ , тогда формула (5) доказана.

Примеры задач по уравнению плоскости

Чтобы ещё лучше понять вышеописанную тему, необходимо решить много задач. Поэтому предлагаем вам ознакомиться с примерами и их решениями.

Составление уравнения плоскости

[stextbox id=”warning” caption=”Пример”]

Задача

Даны точки $M(-4, 6, -6)$ и $N(-9, 2, -5)$ . Составить уравнение плоскости, которая проходит через точку $M$ и перпендикулярна к вектору $\overline{n} = \overline{MN}$ .

Решение

По условию вектор $\overline{n} = \overline{MN}$ – это нормальный вектор плоскости. Найдём его координаты.

$\overline{n}$ = $(-9 - (-4), 2 - 6, -5 - (-6)) = (-5, -4, 1)$ .

Подставляя в уравнение (1) $A = -5, B = -4, C = 1$ , а также $x_{1} = -4, y_{1} = 6, z = -6$

У нас получается:

$-5 (x + 4) - 4(y - 6) + (z + 6) = 0\to{-5x - 4y + z - 10 + 24 + 6 = 0}\to {-5x - 4y + z + 10 = 0$

[/stextbox]

Составление уравнения в отрезках

[stextbox id=”warning” caption=”Пример”]

Задача

Построить плоскость $4x - 2y + 3z - 12 = 0$ и записать её уравнение в отрезках, а также уравнение следов на соответствующих координатных плоскостях.

Решение:

Положим $y = z = 0$ , тогда $4x - 12 = 0\to{x = {12\over{4}}} = 3 = a$ . Аналогично при $x =z = 0$ находим ${y} = {12\over{-2}} = -6 = b$ , при $x = y = 0$ , ${z} = {12\over{3}} = 4 = c$ , тогда уравнение в отрезках запишется:

${x\over{3}} + {y\over{-6}}+ {z\over{4}} = {1}$ (рис. 7)

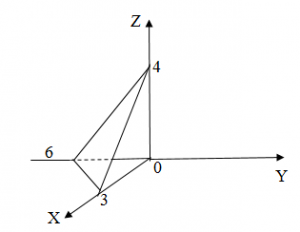
Уравнение плоскости в отрезках

Рис. 7

Уравнение следов:

$4x - 2y -12 = 0, 4x + 3z - 12 = 0, -2y + 3z - 12 = 0$

[/stextbox]

Уравнение плоскости через три точки

[stextbox id=”warning” caption=”Пример”]

Задача

Составить уравнение и построить плоскость, которая проходит через точки $M_{1}(2, 1, 0), M_{2}(0, 1, 2), M_{3}(1, 3, 1)$

Решение

По формуле (4)

$\begin{vmatrix} x-2&y - 1&z - 0\\ 0 - 2&1 - 1&2 - 0\\ 1 - 2&3 - 1&1 - 0 \end{vmatrix} = 0 \to{-4(x - 2) - 0(y - 1) - 4z}= 0\to{x + z - 2 = 0 \right$

Плоскость параллельна $OY$ (рис. 8)

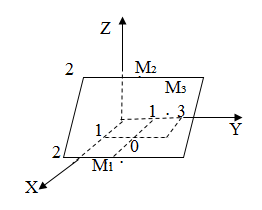
Уравнение плоскости через три точки

Рис. 8

[/stextbox]

Вычисление угла между плоскостями

[stextbox id=”warning” caption=”Пример”]

Задача

Найти угол между плоскостями $2x + 4y - 4z - 6 = 0$ и $4x + 3y + 9 = 0$

Решение

Подставим в формулу вычисления угла между плоскостями соответствующие коэффициенты:

$cos\alpha$ = $|2 * 4 + 4 * 3 + (-4) * 0|\over{\sqrt{2^2 + 4^2 + (-4)^2}} * \sqrt{4^2 + 3^2 + 0^2$ = $|8 + 12|\over\sqrt{36} * \sqrt{25}$ = $20\over30$ = $2\over{3}$

Вы заметили, что в этом примере мы воспользовались исключительно одной формулой? В нашем случае – (5) формула. Никаких других формул мы не использовали и смогли найти угол между двумя плоскостями.

[/stextbox]

Нашли ошибку? Выделите текст и нажмите CTRL + Enter

сагдиана на Решить уравнение с дробями онлайнничего не понятно!
акмарал на Более 50 основных формул по физике с пояснениема эти формулы обычно используют в олимпиядах
всем пока на Решить уравнение с дробями онлайнничего не понятно. калькулятор не работает.
Великий гей Никола Тесла на Более 50 основных формул по физике с пояснениемСайт параша, я пытался списать ЕГЭ по физике с помощью них, я блять сдал его на 99999 балов, и теперь
некто на Примеры решения матриц с ответамиНеправильные ответы, учите матрицу гении

Уравнение плоскости

Уравнение плоскости через точку и нормальный вектор. Общее уравнение плоскости

Исследование общего уравнения плоскостей

Уравнение плоскости в отрезках

Уравнение плоскости проходящей через три точки

Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей

Примеры задач по уравнению плоскости

Составление уравнения плоскости

Составление уравнения в отрезках

Уравнение плоскости через три точки

Вычисление угла между плоскостями

Авторизуйтесь