Прямая линия и плоскость

О чем статья

Угол между прямой и плоскостью

Чтобы найти угол между прямой и плоскостью, необходимо знать определение и несколько основных формул.

Пусть прямая $L$ и плоскость $P$ заданы своими уравнениями:

${x -x_{1}\over{l}} = {y - y_{1}\over{m}} = {z - z_{1}\over{p}}\quad {(L)}$ и $Ax + By + Cz + D = 0\quad {(P)}$

[stextbox id=”info” defcaption=”true”]

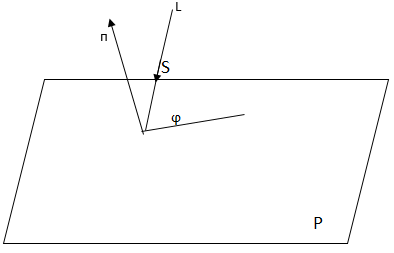
Углом между прямой $L$ и плоскостью $P$ называется угол, созданный этой прямой и её проекцией на эту плоскость $P$ (см. рис. ниже).

[/stextbox]

Обозначим через $\varphi$ величину этого угла. Угол между нормальным вектором $\overline{n} = (A, B, C)$ и направляющим вектором $\overline{S} - (l, m, p)$ равен углу ${\pi\over{2}} - {\varphi}$ , поэтому ${cos(\overline{n}}$ ^ $\overline{S}}})$ = $cos$ x $({\pi\over{2}} - {\varphi}) = {sin \varphi}$ .

Значит,
Угол между прямой и плоскостью

$sin\varphi = cos (\overline{n}$ ,^ $\overline{S})$ = ${\overline{n} * \overline{S}}\over|{\overline{n}| * |\overline{S}}|$ = ${Al + Bm + Cp}\over{\sqrt{A^2 + B^2 + C^2}} * {\sqrt{l^2 + m^2 + p^2}}$

(1)

Из рисунка видно, что $L||P$ , когда $\overline{n}\perp\overline{S}\to\overline{n} * \overline{S} = 0\to$

$Al + Bm + Cp = 0$

(2)

условие параллельности прямой и плоскости.

И если $L\perp{P}$ , тогда $\overline{n}||\overline{S}\to$

${A\over{l}} = {B\over{m}} = {C\over{p}}$

(3)

условие перпендикулярности прямой и плоскости.

Точка пересечения прямой и плоскости

Если прямая $L$ не параллельна плоскости $P$ , тогда они пересекаются в одной точке. Чтобы найти точку пересечения, необходимо решить систему уравнений:

$\left\{ \begin{aligned} {x - x_{1}\over{l}} = {y - y_{1}\over{m}} = {z - z_{1}\over{p}} = t\quad(L)\\ Ax + By + Cz + D = 0\quad(P) \end{aligned} \right$

Это удобнее сделать, если уравнение $(L)$ записать в параметрической форме:

$x = lt + x_{1}, y = mt + y_{1}, z = pt + z_{1}$

(4)

и подставить эти выражения в уравнение $P$ , тогда получим:

$A(lt + x_{1} + B(mt + y_{1}) + C(pt + z_{1}) + D = 0\to$

$t$ = $-{Ax_{1} + By_{1} + Cz_{1} + D\over{Al + Bm + Cp}}.$

За найденным значением $t$ из (4) находим координаты $x, y, z$ точки пересечения.

Примеры решения задач

Примеры помогут закрепить пройденную тему.

[stextbox id=”warning” caption=”Пример 1″]

Задача

Найти угол между прямой ${x - 6\over{2}} = {y + 3\over{-1}} = {z - 8\over{-1}}$ и плоскостью $2x - 4y + 2z + 7 = 0$ .

Решение

Согласно формуле (1) из первого уравнения находим направляющий вектор $\overline{S} = (2, -1, -1)$ , из уравнения плоскости – нормальный вектор $\overline{n} = (2, -4, 2)$ , тогда

$sin \varphi$ = $\overline{n} * \overline{S}\over|\overline{n}| * |\overline{S}|$ = ${2 * 2 + (-1)(-4) + (-1) * 2}\over{\sqrt{2^2 + (-1)^2 + (-1)^2}} * {\sqrt{2^2 + (-4)^2 + 2^2}}$ = $6\over{\sqrt{6}} * {\sqrt{24}}$ = ${1\over{2}}$ ,

Ответ

$\varphi = arcsin{1\over{2}} = 30^0.$

[/stextbox]

[stextbox id=”warning” caption=”Пример 2″]

Задача

Составить уравнение плоскости, которая проходит через точку $A(-3, 4, -7)$ и перпендикулярна прямой ${x + 4\over{3}} = {y - 1\over{-2}} = {z - 4\over{6}}$ .

Решение

Согласно условию (3) перпендикулярности прямой и плоскости $(\overline{S}||\overline{n})$ за нормальный вектор можно взять параллельный ему направляющий вектор прямой $\overline{S} = (3, -2, 6)$ . Используя уравнение плоскости, которая проходит через точку $A(-3, 4, -7)$ перпендикулярна вектору $\overline{n} = (3, -2, 6)$ у нас получается:

Ответ $3 (x + 3) + (-2)(y - 4) + 6(z + 7) = 0\to3x - 2y + 6z + 43 = 0$ .

[/stextbox]

Для наглядности покажем ещё несколько примеров, где необходимо найти точку пересечения с плоскостью.

[stextbox id=”warning” caption=”Пример 3″]

Задача

Найти точку пересечения прямой ${x - 1\over{2}} = {y + 2\over{1}} = {z\over{3}}$ с плоскостью $2x + 3y - 3z - 6 = 0$

Решение

Запишем уравнение прямой в параметрическом виде: $x = 2t + 1, y = t - 2, z = 3t$ . Подставим выражения для $x, y, z$ в общее уравнение плоскости $2(2t + 1) + 3(t - 2) - 3 * 3t - 6 = 0\to4t + 3t - 9t - 10 = 0\to -2t = 10, t = -5$ Откуда

$x = 2 * (-5) + 1 = -9, y = -5 - 2 = -7, z = - 15; \quad{M(-9, -7, -15)}.$

Ответ

$x = 2 * (-5) + 1 = -9, y = -5 - 2 = -7, z = - 15; \quad{M(-9, -7, -15)}.$

[/stextbox]

[stextbox id=”warning” caption=”Пример 4″]

Задача

Найти точку $N$ симметричную с точкой $M(-1, 4, 2)$ относительно плоскости $3x + y + z - 14 = 0$ .

Решение

Сначала составим уравнение прямой , которая проходит через точку $M(-1, 4, 2)$ перпендикулярно к плоскости. За направляющий вектор $\overline{S}$ можно взять нормальный вектор $\overline{n} = (3, 1, 1)$ данной плоскости (см. условию (3).

Значит, у нас получается: ${x + 1\over{3}} = {y - 4\over{1}} = {z - 2\over{1}}\quad(=t)$

Найдём точку пересечения найденной прямой с плоскостью. Из уравнения прямой выражаем $x = 3t - 1, y = t + 4, z = t + 2$ и подставляем в уравнение плоскости:

$3(3t - 1) + (t + 4) + (t + 2) - 14 = 0\to11t - 11 = 0\to{t} = 1$ ;

$x = 3 * 1 - 1 = 2, y = 1 + 4 = 5, z = 1 + 2 = 3\to{Q}(2, 5, 3)$ – точка пересечения прямой и плоскости. Эта точка между двумя симметричными относительно плоскости точкам $M(-1, 4, 2)$ и $N(X_{n}, Y_{n}, Z_{n})$ , то есть:

$x_{Q}$ = ${x_{M} + x_{N}\over{2}}\to{x_{N}} = 2x_{Q} - x_{M} = 2 * 2 - (-1) = 5$ ;

$y_{Q}$ = ${y_{M} + y_{N}\over{2}}\to{y_{N}} = 2 * 5 - 4 = 6$ ;

$z_{N}$ = $2 * 3 - 2 = 4$ .

Ответ

Симметричной с точкой $M (-1, 4, 2)$ относительно заданной плоскости есть точка $N(5, 6, 4)$ .

[/stextbox]

Нашли ошибку? Выделите текст и нажмите CTRL + Enter

сагдиана на Решить уравнение с дробями онлайнничего не понятно!
акмарал на Более 50 основных формул по физике с пояснениема эти формулы обычно используют в олимпиядах
всем пока на Решить уравнение с дробями онлайнничего не понятно. калькулятор не работает.
Великий гей Никола Тесла на Более 50 основных формул по физике с пояснениемСайт параша, я пытался списать ЕГЭ по физике с помощью них, я блять сдал его на 99999 балов, и теперь
некто на Примеры решения матриц с ответамиНеправильные ответы, учите матрицу гении